Дифференциальное уравнение движения механической системы в обобщенных координатах (уравнение Лагранжа 2-го рода)
Полагаем, что механическая система состоит из n -точек, имеет S -степеней свободы. Рассмотрим движение i -точки, которое опишем радиус–вектором
Тогда скорость i -точки
При условии стационарных связей
Уравнение (1) также называют тождеством Лагранжа. Теперь рассмотрим кинетическую энергию системы. Она есть функция обобщенных координат, обобщенных скоростей и времени.
Для системы точек:
Вычисляем частное производную по
Подставляя уравнения (1), получаем:
Возьмем полный дифференциал по t:
Уравнение (3) является дифференциальным уравнением системы в обобщенных координатах или уравнением Лагранжа 2 рода. Количество этих уравнений зависит от числа степеней свободы s. Алгоритм решения задач с применением уравнения Лагранжа 2 рода можно разбить на 6 пунктов: 1) выбрать обобщенную координату и определить число степеней свободы s; 2) вычислить кинетическую энергию системы через обобщенную координату; 3) записать уравнение Лагранжа 2 рода в соответствии с выбранной обобщенной координатой; 4) дифференцируем в соответствии с уравнением; 5) определяем обобщенную силу, соответствующую выбранной обобщенной координате. Для этого сначала надо определить потенциальную энергию системы или работу системы:
6) все найденные величины подставить в уравнение Лагранжа.
|

 , который является функцией обобщенных координат и времени:
, который является функцией обобщенных координат и времени:
 :
:
 . Тогда, продифференцировав по
. Тогда, продифференцировав по  , получим:
, получим: (1)
(1)

 по q и по t:
по q и по t:
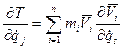
 (2)
(2)
 (3)
(3) ;
;


