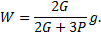Принцип возможных перемещений и общее уравнение динамики для неголономных и голономных систем в обобщенных координатах.
По принципу Даламбера материальную систему, движущуюся под действием некоторых сил, можно рассматривать находящейся в равновесии, если ко всем точкам системы приложить их силы инерции. Значит можно воспользоваться и принципом возможных перемещений. В уравнение работ (1) добавится еще сумма работ сил инерции точек на их возможных перемещениях:
Или по принципу возможных скоростей (2):
Эти уравнения называют общим уравнением динамики. Оно позволяет решать большой класс задач на исследование движения довольно сложных материальных систем. Уравнения (3) и (4) показывают, что в любой фиксированный момент времени сумма элементарных работ активных сил и сил инерции на любых виртуальных перемещениях равна нулю при условии, что на систему наложены идеальные и удерживающие связи. Силы инерции точек и твердых тел, составляющих систему, определять уже умеем. Стоит подчеркнуть еще одно важное достоинство этого метода, общего уравнения динамики, – реакции связей (идеальных) исключаются при исследовании движения системы. Иногда это уравнение можно использовать для исследования движения механических систем и в тех случаях, когда не все связи являются идеальными, например, когда имеются связи с трением. Для этого следует к активным силам добавить те составляющие реакций, которые обусловлены наличием сил трения. Рассмотрим процедуру использования уравнения (3) для составления дифференциальных уравнений движения систем с двумя степенями свободы: 1. Изобразить механическую систему в произвольный момент времени. 2. Показать на рисунке активные силы и моменты, а также силы и моменты, соответствующие неидеальным связям (например, силы трения). 3. Определить главные векторы и главные моменты сил инерции. 4. Выбрать обобщенные координаты в числе, равном числу степеней свободы системы. 5. Дать виртуальное перемещение, соответствующее одной из степеней свободы системы, считая при этом виртуальные перемещения, соответствующие остальным степеням свободы, равными нулю. 6. Вычислить сумму элементарных работ всех сил и моментов (см. п. 2 и 3) на соответствующих виртуальных перемещениях и приравнять эту сумму нулю. 7. Повторить п. 4 - 6 для каждого независимого движения системы. При применении общего уравнения динамики к системам с двумя и большим числом степеней свободы, в связи с громоздкостью выкладок, можно использовать следующие рекомендации: 1. Сделать предположение о направлении ускорений точек системы. 2. Направить на рисунке силы инерции в стороны, противоположные выбранным направлениям соответствующих ускорений. 3. Определить знаки элементарных работ сил инерции в соответствии с их направлениями на рисунке и избранными направлениями виртуальных перемещений точек системы. 4. Если искомые ускорения оказываются положительными, то сделанные предположения о направлениях ускорений подтверждаются, если отрицательными, то соответствующие ускорения направлены в другую сторону.
Пример 3. Определим ускорение груза G (рис.6). Вес цилиндра – Р, радиус – r. Цилиндр катится по плоскости без скольжения.
Рис.6
Решение. Показываем задаваемые силы –
Цилиндр совершает плоскопараллельное движение. Главный вектор сил инерции точек его
Главный момент сил инерции относительно центральной оси С:
Даем системе возможное перемещение, сдвинув груз вниз на малую величину
Вычисляем работу сил на этих перемещениях и составляем уравнение работ, общее уравнение динамики,
Так как
из которого находим
|

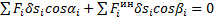 . (3)
. (3)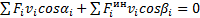 (4)
(4)
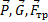 . Добавляем силы инерции. Сила инерции груза, движущегося поступательно,
. Добавляем силы инерции. Сила инерции груза, движущегося поступательно,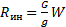 .
.


 . Центр цилиндра сместится вправо на величину
. Центр цилиндра сместится вправо на величину  , а весь цилиндр повернется вокруг мгновенного центра скоростей
, а весь цилиндр повернется вокруг мгновенного центра скоростей 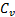 на угол
на угол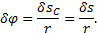
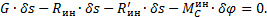
 , то, подставив значения сил инерции, получим уравнение
, то, подставив значения сил инерции, получим уравнение