Плоская система сил. Приведение к простейшей системе. Три формы уравнении равновесия для плоской системы
7.1 Алгебраические моменты сил и пары сил 7.1.1 Алгебраический момент силы относительно центра Когда все силы системы лежат в одной плоскости, их моменты относительно любого центра O, находящегося в той же плоскости, перпендикулярны этой плоскости, т.е. направлены вдоль одной и той же прямой. Тогда не прибегая к векторной символике, можно направление этих моментов отличать одно от другого и рассматривать момент силы Алгебраический момент силы
Момент считается положительным, если сила стремится повернуть тело вокруг центра O против хода часовой стрелки и отрицательным – если по ходу часовой стрелки. Так, для сил изображенных на рисунке 7.1:
Рисунок 7.1 Следует отметить, полученные формулы (6.5) и (6.7), содержащие суммы моментов-векторов, сохраняет свой вид и для алгебраических моментов, но суммы при этом будут не векторные, а алгебраические. 7.1.2 Алгебраический момент пары Поскольку момент пары сил равен моменту одной из ее сил относительно точки приложения другой силы, то для пар, лежащих в одной плоскости, момент пары можно рассматривать как алгебраическую величину, называть алгебраическим моментом пары и обозначать символом m (или M). При этом, алгебраический момент пары равен взятому с соответствующим знаком произведению модуля одной из сил пары на плечо пары:
Правило знаков здесь такое же, как и для момента силы. Так для изображенной на рисунке 7.2а, пары
Рисунок 7.2 Поскольку пара сил характеризуется только ее моментом, то на рисунках пару изображают просто дуговой стрелкой, показывающей направление поворота пары (как на рисунке 7.2 б). Полученные ранее формулы, содержащие суммы моментов-векторов, тоже сохраняют вид для алгебраических моментов, причем суммы будут алгебраическими.
7.2 Приведение плоской системы сил к простейшему виду Результат, полученный в разделе 6.1 справедлив и для плоской системы сил. Следовательно, плоская система сил тоже приводится к силе, равной
Рисунок 7.3 Значения главного вектора При этом вектор
где все моменты в последнем равенстве алгебраические и сумма тоже алгебраическая. Найдем, к какому простейшему виду может приводиться плоская система сил, не находящихся в равновесии. Результат зависит от значения 1. Если для данной системы сил 2. Если a. b.
Отбросив теперь силы 1) расстояние 2) знак момента относительно центра O силы Таким образом, плоская система сил, не находящихся в равновесии может быть окончательно приведена или к одной силе 7.3 Равновесие плоской системы сил. Случай параллельных сил Необходимые и достаточные условия равновесия любой системы сил даются равенствами Найдем вытекающие отсюда аналитические условия равновесия плоской системы сил. Их можно получить в трех различных формах.
7.3.1 Основная форма условий равновесия Так как вектор
Формулы (7.5) выражают аналитические условия равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю. Одновременно равенства (7.5) выражают условия равновесия твердого тела, находящегося под действием плоской системы сил.
7.3.2 Вторая форма условий равновесия Вторая форма условий равновесия: для равновесия произвольной плоской системы сил необходимо о достаточно, чтобы суммы моментов всех этих сил относительно каких-нибудь двух центров А и В и сумма их проекций на ось ОХ, не перпендикулярную прямой АВ, были равны нулю: 1) Необходимость этих условий очевидна, т.к. если любое из них не выполняется, то или Докажем их достаточность. Если для данной системы сил выполняются только первые два из условий (7.6), то есть для нее
7.3.3 Третья форма условий равновесия (уравнение трех моментов) Третья форма условий равновесия (уравнение трех моментов): для равновесия произвольной плоской системы сил необходимо о достаточно, чтобы суммы моментов всех этих сил относительно любых трех центров А, В и С, не лежащих на одной прямой, были равны нулю: 1) Необходимость этих условий очевидна, как и в предыдущем случае. Достаточность условия следует из того, что если при одновременном выполнении этих условий данная система сил не находилась бы в равновесии, то она должна была бы приводиться к равнодействующей, проходящей через точки А, В и С, что невозможно, т.к. эти точки не лежат на одной прямой. Во всех рассмотренных случаях для плоской системы сил получаются три условия равновесия. Условия (7.5) считаются основными, так как при пользовании ими никаких ограничений на выбор координатных осей и центра моментов не налагается.
7.4 Равновесие плоской системы параллельных сил В случае, когда все действующие на тело силы параллельно друг другу, можно направить ось Ох перпендикулярно силам, а ось Оу параллельно им (рисунок 7.4). Тогда проекция каждой из сил на ось Ох будет равна нулю и первое из равенств (7.5) обратится в тождество вида 1)
Рассмотрим некоторые частные случаи предыдущей теоремы.
Таким образом, плоская система сил, если она не находится в равновесии, приводится или к одной равнодействующей (когда R ¹ 0) или к одной паре (когда R = 0).
Пример 2.К диску приложены силы:
Rx = åFix = -F1cos300 – F2cos300 +F4cos450 = 0; Рис. 3.16 Ry = åFiy = -F1cos600 + F2cos600 – F3 + F4cos450 = 0. Поэтому R = 0. Главный момент системы М0:
Ответ: R = 0; М0 = 0; тело находится в равновесии.
Пример 3.
Модуль главного вектора R равен: Направляющие косинусы будут:
mA = mA(F1) + mA(F2) + mA(F3).
mA = mA(F2) = F*a. Таким образом система сил приведена к силе R и паре сил с моментом mA, направленном против часовой стрелки (рис. 3.18). Ответ: R = 2F; (х,^ R) = 1500; (y,^ R) = 600; mA = F*a. Плоская система сил может быть приведена к главному вектору и главному моменту. Поэтому условия равновесия сил на плоскости, как показано выше, имеет вид:
Мо = Итак, для равновесия системы сил, произвольно расположенных в плоскости, необходимо и достаточно, чтобы главный вектор и главный момент этих сил относительно любого центра каждый в отдельности равнялся нулю. Главный вектор R' = Для равновесия необходимо, чтобы главный вектор был равен нулю; при соблюдении этого условия получим:
Кроме того, для равновесия необходимо, чтобы главный момент также был равен нулю, т.е.
В дальнейшем для уравнений равновесия при решении задач будем применять более компактную форму записи: вместо Уравнения равновесия произвольной плоской системы сил могут быть представлены в трех формах. Первая – основная форма этих уравнений – выведена выше:
Зачастую при решении задач рациональнее пользоваться другими формами уравнений равновесия. Так как при равновесии твердого тела сумма моментов всех приложенных к нему сил относительно любой точки равна нулю, то можно, выбрав три произвольные точки А, В, С и приравняв нулю сумму моментов относительно каждой из них, получить три следующих уравнения равновесия:
Это вторая форма уравнений равновесий. Точки А, В, С не должны лежать на одной прямой. Третья форма уравнений равновесия представляет собой равенство нулю сумм моментов относительно двух произвольных точек А и В и равенство нулю суммы проекций на некоторую ось х:
При пользовании этой формой уравнений равновесия необходимо, чтобы ось х не была перпендикулярна линии, соединяющей точки А и В. Для системы параллельных сил, выбрав одну из осей проекций, параллельной этим силам, а другую – перпендикулярной к ним, получим существенные упрощения (рис. 21).
Рис. 21 Первая форма уравнений равновесия для плоской системы параллельных сил примет вид:
Вторая и третья формы уравнений равновесия для плоской системы параллельных сил примут одинаковый вид:
Итак, для произвольной плоской системы сил имеем уравнения равновесия; а для плоской системы параллельных сил – только две. Соответственно при решении задач на равновесие произвольной плоской системы сил можно найти три неизвестных, а при рассмотрении равновесия плоской системы параллельных сил – не более двух. Если количество неизвестных превышает число уравнений статики, задача становится статически неопределимой. Методы решения таких задач рассматриваются в курсе сопротивления материалов.
|

 относительно центра O как алгебраическую величину, которую будем обозначать
относительно центра O как алгебраическую величину, которую будем обозначать 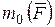 .
. (7.1)
(7.1)

 (7.2)
(7.2) момент
момент  ; а для
; а для  и
и 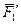 момент
момент  .
.

 и приложенной в произвольно выбранной точке O, и паре с моментом M0, но сила и пара лежат в данном случае в одной плоскости – плоскости действия сил (рисунок 7.3 а, где пара изображена дуговой стрелкой).
и приложенной в произвольно выбранной точке O, и паре с моментом M0, но сила и пара лежат в данном случае в одной плоскости – плоскости действия сил (рисунок 7.3 а, где пара изображена дуговой стрелкой).
 .
. (7.3)
(7.3) , а
, а 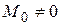 , то она приводится к одной паре с моментом M0, значение M0 не зависит от выбора центра O.
, то она приводится к одной паре с моментом M0, значение M0 не зависит от выбора центра O. для данной системы сил, то она приводится к одной силе, т.е. к равнодействующей, при этом возможны два случая:
для данной системы сил, то она приводится к одной силе, т.е. к равнодействующей, при этом возможны два случая: ,
,  . В этом случае система приводится к равнодействующей, проходящей через точку O;
. В этом случае система приводится к равнодействующей, проходящей через точку O; и
и  , беря
, беря  , а
, а  (рисунок 7.3 б). При этом, если
(рисунок 7.3 б). При этом, если  , то
, то (7.4)
(7.4) и
и 
 должно удовлетворять равенству 7.4.;
должно удовлетворять равенству 7.4.; , должны совпадать со знаком M0.
, должны совпадать со знаком M0. ) или к паре сил (когда
) или к паре сил (когда 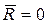 ).
). и
и  .
. равен нулю, когда равны нулю его проекции
равен нулю, когда равны нулю его проекции 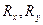 , то для равновесия должны выполняться равенства
, то для равновесия должны выполняться равенства  , а также
, а также  , где
, где  – алгебраический момент, а точка О – любая точка в плоскости действия сил, но предыдущие равенства будут выполняться, когда действующие силы удовлетворяют условиям:
– алгебраический момент, а точка О – любая точка в плоскости действия сил, но предыдущие равенства будут выполняться, когда действующие силы удовлетворяют условиям: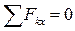 ;
;  ;
;  (7.5)
(7.5) ; 2)
; 2)  ; 3)
; 3)  (7.6)
(7.6) и равновесия не будет.
и равновесия не будет. и
и  , то система сил может иметь равнодействующую
, то система сил может иметь равнодействующую  , одновременно проходящую через точки А и В – значит система не находится в равновесии. Так как ось ОХ проведена не перпендикулярно к АВ, то это возможно только тогда, когда
, одновременно проходящую через точки А и В – значит система не находится в равновесии. Так как ось ОХ проведена не перпендикулярно к АВ, то это возможно только тогда, когда  , т.е. когда имеет место равновесие.
, т.е. когда имеет место равновесие. (7.7)
(7.7) . в результате для параллельных сил останется два условия равновесия
. в результате для параллельных сил останется два условия равновесия ; 2)
; 2)  (7.8)
(7.8)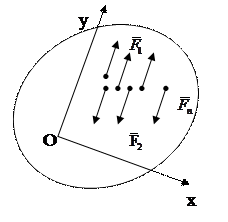
 1. Если для данной системы сил R = 0, M0 = 0, то она находится в равновесии.
1. Если для данной системы сил R = 0, M0 = 0, то она находится в равновесии.
 2. Если для данной системы сил R = 0, M0 ¹ 0, то она приводится к одной паре с моментом M0 = åm0(Fi). В этом случае величина M0 не зависит от выбора центра О.
2. Если для данной системы сил R = 0, M0 ¹ 0, то она приводится к одной паре с моментом M0 = åm0(Fi). В этом случае величина M0 не зависит от выбора центра О.

 3. Если для данной системы сил R ¹ 0, то она приводится к одной равнодействующей, причем если R ¹ 0 и M0 = 0, то система заменяется одной силой, т.е. равнодействующей R, проходящей через центр О; в случае если R ¹ 0 и M0 ¹ 0, то система заменяется одной силой, проходящей через некоторую точку С, причем ОС = d(OC^R) и d = |M0|/R.
3. Если для данной системы сил R ¹ 0, то она приводится к одной равнодействующей, причем если R ¹ 0 и M0 = 0, то система заменяется одной силой, т.е. равнодействующей R, проходящей через центр О; в случае если R ¹ 0 и M0 ¹ 0, то система заменяется одной силой, проходящей через некоторую точку С, причем ОС = d(OC^R) и d = |M0|/R.
 (рис. 3.16) привести эту систему сил к простейшему виду.
(рис. 3.16) привести эту систему сил к простейшему виду. Решение: выберем систему координат Оху. За центр приведения выберем точку О. Главный вектор R:
Решение: выберем систему координат Оху. За центр приведения выберем точку О. Главный вектор R:




 ;
; .
.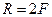 .
. ;
;  .
. Отсюда: (х, R) = 1500; (y, R) = 600.
Отсюда: (х, R) = 1500; (y, R) = 600. Определим главный момент системы сил относительно центра приведения А. Тогда
Определим главный момент системы сил относительно центра приведения А. Тогда Учитывая, что mA(F1) = mA(F3) = 0, так как направление сил проходит через точку А, тогда
Учитывая, что mA(F1) = mA(F3) = 0, так как направление сил проходит через точку А, тогда
 ' = 0;
' = 0; o(
o( i) = 0. (20)
i) = 0. (20) и
и  , получим для величины главного вектора выражение
, получим для величины главного вектора выражение .
. = 0; вместо
= 0; вместо  o = 0.
o = 0. = 0;
= 0; 



