Сложения пар, произвольно расположенных в пространстве . простейшая система для системы пар сил. условие равновесия системы пар сил.
Свойства пар сил определяются рядом теорем, которые приводятся без доказательств: · Две пары эквивалентны, если их векторные моменты равны по величине и одинаково направлены. · Действие пары на тело не изменится, если ее перенести в плоскости действия на любое место. · Действие пары на тело не изменится, если ее перенести из плоскости действия в параллельную ей плоскость. · Действие пары на тело не изменится, если увеличить (уменьшить) величину силы пары, одновременно уменьшая (увеличивая) во столько же раз плечо пары. Вывод: векторный момент пары сил, действующей на твердое тело, есть свободный вектор, т. е. его можно приложить в любой точке твердого тела. Рассмотрим сложение пар, произвольно расположенных в пространстве. Докажем теорему: Система пар, произвольно расположенных в пространстве, эквивалентна одной паре с моментом, равным геометрической сумме моментов слагаемых пар. Возьмем две пары (
Рис.2.18 Равнодействующая пар сил Систему пар сил, действующих на тело, можно, в соответствии с только что доказанной теоремой, заменить одной парой, равной сумме векторов моментов слагаемых пар. Следовательно, равновесие системы пар возможно только при выполнении условия
Проецируя приведенное векторное условие равновесия пар на любые три оси, не лежащие в одной плоскости и не параллельные друг другу, получим скалярные уравнения равновесия системы пар Если на тело, закрепленное в некоторой точке А, действует сила F, то тело повернется относительно этой точки. Вращательное движение тела характеризуется вращающим моментом М. Моментом силы F относительно точки А называется величина, численно равная произведению силы на плечо (рис. 1.16):
Парой сил называется система двух сил, равных по величине, противоположных по направлению и не лежащих на одной Пара сил оказывает на тело вращающее действие, которое характеризуется вращающим моментом М. Вращающий момент пары сил равен произведению одной из сил пары на плечо:
Условие равновесия плоской системы пар сил:алгебраическая сумма моментов слагаемых пар сил должна быть равна нулю, т.е.
|

 ) и (
) и ( ), расположенные на пересекающихся под произвольным углом плоскостях. Плечи пар примем равными соответственно
), расположенные на пересекающихся под произвольным углом плоскостях. Плечи пар примем равными соответственно  и
и  . На линии пересечения плоскостей отметим произвольный отрезок АВ и приведем каждую из слагаемых пар к плечу АВ. Произведя сложение соответствующих сил (см. рис.)
. На линии пересечения плоскостей отметим произвольный отрезок АВ и приведем каждую из слагаемых пар к плечу АВ. Произведя сложение соответствующих сил (см. рис.)  с
с  и
и 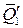 с
с  , получим новую пару (
, получим новую пару (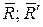 ), момент которой будет равен
), момент которой будет равен



 где l — плечо (перпендикуляр, опущенный из точки на линию действия силы). За единицу вращающего момента принимается 1 Нм: 1кНм=103Нм.
где l — плечо (перпендикуляр, опущенный из точки на линию действия силы). За единицу вращающего момента принимается 1 Нм: 1кНм=103Нм. прямой (рис. 1.17).
прямой (рис. 1.17).
 где h — плечо пары сил (перпендикуляр, восстановленныймежду линиями действия сил). Пара сил на схемах изображается дугообразной стрелкой (рис. 1.18). Пару сил нельзя заменить одной равнодействующей силой. Пара сил не имеет проекций на оси координат. Если на тело действует несколько пар сил, то их можно заменить одной равнодействующей парой, момент которой равен алгебраической сумме моментов слагаемых пар сил, действующих на тело (рис. 1.19):
где h — плечо пары сил (перпендикуляр, восстановленныймежду линиями действия сил). Пара сил на схемах изображается дугообразной стрелкой (рис. 1.18). Пару сил нельзя заменить одной равнодействующей силой. Пара сил не имеет проекций на оси координат. Если на тело действует несколько пар сил, то их можно заменить одной равнодействующей парой, момент которой равен алгебраической сумме моментов слагаемых пар сил, действующих на тело (рис. 1.19):

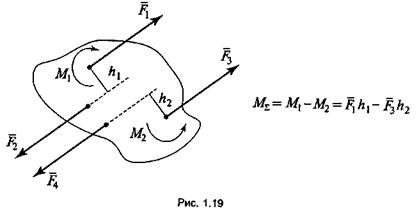 Две пары сил называются эквивалентными,если они оказывают на тело одинаковое действие. У эквивалентных пар сил вращающие моменты должны быть одинаковы как по величине, так и по направлению.
Две пары сил называются эквивалентными,если они оказывают на тело одинаковое действие. У эквивалентных пар сил вращающие моменты должны быть одинаковы как по величине, так и по направлению.



