Понятие о паре сил. характеристики пары. Задание пары. Момент пары сил как вектор.
Парой сил называются две равные и параллельные силы, не лежащие на одной прямой и направленные в противоположные стороны. Пара сил имеет важное значение в практике. Так, водитель автомобиля, передавая руками усилия на рулевое колесо, использует пару сил. Сумма проекций сил пары на любую ось равна нулю (рис. 1), т.е. пара сил не имеет равнодействующей. Однако, несмотря на это, под действием пары сил тело не находится в равновесии.
Рис. 1.
Пара сил, действуя на тело, стремится вращать его, что определяется моментом пары (моментом силы). Понятие момента пары ввел в механику итальянский ученый и художник эпохи Возрождения Леонардо да Винчи. Моментом силы относительно точки называется произведение модуля силы на ее плечо, т.е.
Точка, относительно которой берется момент, называется центром момента. Плечом силы относительно точки называется кратчайшее расстояние от центра момента до линии действия силы. Единица измерения момента силы:
Эффект действия пары сил определяется ее моментом, поэтому пару сил принято изображать дугой (или другим знаком, обозначающим вращение), указывающей направление вращения. Момент силы принято считать положительным, если сила стремится повернуть тело по ходу часовой стрелки (рис. 8, а), и отрицательным, если сила стремится вращать тело против хода часовой стрелки (рис. 8, б). Однако принятое правило знаков условно. Можно принять и противоположное правило. Одна и та же сила относительно разных точек может давать и положительный, и отрицательный момент. Момент силы относительно точки, лежащей на линии действия этой силы, равен нулю. Эквивалентность пар. По аналогии с определением эквивалентных систем сил две пары сил считаются эквивалентными, если одну из них можно заменить другой, не нарушая механического состояния свободного твердого тела. Эффект действия пары сил на твердое тело не зависит от ее положения в плоскости. Таким образом, пару сил можно переносить в плоскости ее действия в любое положение. Основой для сложения пары сил является следующее ее свойство: не нарушая механического состояния тела, можно менять силы и плечо пары, но так, чтобы ее момент оставался неизменным. Сложение пар. Подобно силам пары сил можно складывать. Пара, заменяющая собой действие заданных пар, называется результирующей. Сложим две пары, расположенные в одной плоскости. Имеем пары
с плечами а и b (рис. 2), т.е.
Рис. 2 Преобразуем данные пары так, чтобы их плечи были равны при сохранении величин их моментов. Примем за общее плечо преобразованных пар отрезок АВ = с и обозначим
силы эквивалентных пар. Тогда
Складывая силы, приложенные в точках А и В, найдем их равнодействующие:
Равнодействующие R и R', равные по величине и направленные в разные стороны, образуют пару сил
Пара
а так как
Таким образом, момент результирующей пары сил равен алгебраической сумме моментов составляющих пар. При произвольном количестве моментов имеем
На основании правила сложения пар устанавливается условие равновесия системы пар, лежащих в одной плоскости: для равновесия плоской системы пар необходимо и достаточно, чтобы алгебраическая сумма моментов данных пар равнялась нулю, т.е.
Свойства пар сил определяются рядом теорем, которые приводятся без доказательств: · Две пары эквивалентны, если их векторные моменты равны по величине и одинаково направлены. · Действие пары на тело не изменится, если ее перенести в плоскости действия на любое место. · Действие пары на тело не изменится, если ее перенести из плоскости действия в параллельную ей плоскость. · Действие пары на тело не изменится, если увеличить (уменьшить) величину силы пары, одновременно уменьшая (увеличивая) во столько же раз плечо пары. Вывод: векторный момент пары сил, действующей на твердое тело, есть свободный вектор, т. е. его можно приложить в любой точке твердого тела. Рассмотрим сложение пар, произвольно расположенных в пространстве. Докажем теорему: Система пар, произвольно расположенных в пространстве, эквивалентна одной паре с моментом, равным геометрической сумме моментов слагаемых пар. Возьмем две пары (
Рис.2.18 Равнодействующая пар сил Систему пар сил, действующих на тело, можно, в соответствии с только что доказанной теоремой, заменить одной парой, равной сумме векторов моментов слагаемых пар. Следовательно, равновесие системы пар возможно только при выполнении условия
Проецируя приведенное векторное условие равновесия пар на любые три оси, не лежащие в одной плоскости и не параллельные друг другу, получим скалярные уравнения равновесия системы пар Рис.37 1. Изображение момента вектором. Момент силы 1) модулем момента, равным произведению модуля силы на плечо, т. е. Но в случае сил, произвольно расположенных в пространстве, плоскости поворота у разных сил будут разными и должны задаваться дополнительно. Положение плоскости в пространстве можно задать, задав отрезок (вектор), перпендикулярный к этой плоскости. Если одновременно модуль этого вектора выбрать равным модулю момента силы и условиться направлять этот вектор так, чтобы его направление определяло направление поворота силы, то такой вектор полностью определит все три элемента, характеризующие момент данной силы относительно центра О. Поэтому в общем случае момент 2. Выражение момента силы с помощью векторного произведения. Рассмотрим векторное произведение так как модуль вектора
где вектор Таким образом, момент силы
Действие пары сил на тело характеризуется: 1) величиной модуля момента пары, 2) плоскостью действия, 3) направлением поворота в этой плоскости. При рассмотрении пар, не лежащих в одной плоскости, для характеристики каждой из пар необходимо будет задать все эти три элемента. Это можно сделать, если условиться, по аналогии с моментом силы, изображать момент пары соответствующим образом, построенным вектором, а именно: будем изображать момент пары вектором т илиМ, модуль которого равен (в выбранном масштабе) модулю момента пары, т.е. произведению одной из ее сил на плечо, и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда поворот пары виден происходящим против хода часовой стрелки (рис. 38).
|










 , момент которой будет:
, момент которой будет:
 представляет собой результирующую пару. Подставив в уравнение момента М значение равнодействующей R, получим
представляет собой результирующую пару. Подставив в уравнение момента М значение равнодействующей R, получим



 ) и (
) и ( ), расположенные на пересекающихся под произвольным углом плоскостях. Плечи пар примем равными соответственно
), расположенные на пересекающихся под произвольным углом плоскостях. Плечи пар примем равными соответственно  и
и  . На линии пересечения плоскостей отметим произвольный отрезок АВ и приведем каждую из слагаемых пар к плечу АВ. Произведя сложение соответствующих сил (см. рис.)
. На линии пересечения плоскостей отметим произвольный отрезок АВ и приведем каждую из слагаемых пар к плечу АВ. Произведя сложение соответствующих сил (см. рис.)  с
с  и
и 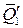 с
с  , получим новую пару (
, получим новую пару (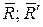 ), момент которой будет равен
), момент которой будет равен



 относительно центра О (см. рис. 37) как характеристика ее вращательного эффекта определяется следующими тремя элементами:
относительно центра О (см. рис. 37) как характеристика ее вращательного эффекта определяется следующими тремя элементами: ; 2) плоскостью поворота ОАВ, проходящей через линию действия силы
; 2) плоскостью поворота ОАВ, проходящей через линию действия силы  , где знак указывает направление поворота.
, где знак указывает направление поворота. ) силы
) силы  , равным по модулю (в выбранном масштабе) произведению модуля силы
, равным по модулю (в выбранном масштабе) произведению модуля силы  определяет положение центра момента.
определяет положение центра момента. x
x  ,
, . Направлен вектор (
. Направлен вектор ( или
или  ,
, =
=  , соединяющего центр О с точкой приложения силы А, на саму силу. Этим выражением момента силы бывает удобно пользоваться при доказательстве некоторых теорем.
, соединяющего центр О с точкой приложения силы А, на саму силу. Этим выражением момента силы бывает удобно пользоваться при доказательстве некоторых теорем.



