Аксиомы статики твердого тела .аксиомы уравновешенной системы двух сил . аксиома параллелограмма сил. Сила, как скользящий вектор
Абсолютно твердым телом* называется материальное тело, в котором расстояния между точками остаются неизменными независимо от действующих сил. Несмотря на такую абстракцию, методами статики твердого тела могут быть решены задачи о равновесии реальных деформируемых тел.
Совокупность сил, приложенных к одному или нескольким твердым телам, называется системой сил. Системы сил, оказывающие на твердое тело одинаковые действия, называются эквивалентными системами. Если существует одна сила, эквивалентная некоторой системе, то она называется равнодействующей этой системы. Твердое тело, которое может занимать в пространстве любое произвольное положение, называется свободным. Если же свобода перемещения тела в пространстве ограничена другими телами, то данное тело называется несвободным, а ограничивающие его тела - связями. Силы, с которыми связи действуют на данное тело, называются реакциями связей. Например, опоры моста, на которые опирается пролетное строение, являются для последнего связями, а силы, с которыми они действуют на пролетное строение – реакциями этих опор. Силы, не являющиеся реакциями связей, называются задаваемыми, или активными. Система сил называется уравновешенной, если ее приложение к покоящемуся свободному твердому телу не нарушает его состояния покоя. Силы, приложенные к телу во всех точках части поверхности или во всех точках объема тела, называются распределенными. Если же сила приложена в одной точке, то она называется сосредоточенной. Реально все силы в природе являются распределенными, сосредоточенные же силы есть равнодействующие некоторых распределенных. Например, реакцию рельса, действующую на колесо, иногда представляют в виде сосредоточенной силы, хотя в действительности колесо и рельс соприкасаются не в одной точке, а по некоторой площадке. Примерами распределенных сил могут служить сила тяжести, сила давления воды, давление ветра, сыпучих грузов и т.д. При решении задач статики часто целесообразно распределенную нагрузку заменять одной эквивалентной сосредоточенной силой. Рассмотрим некоторые простейшие примеры распределенных сил, лежащих в одной плоскости. Плоская система распределенных сил характеризуется ее интенсивностью
В частном случае сил, распределенных вдоль отрезка прямой, значения эквивалентных сосредоточенных сил могут быть найдены по формулам, определяющим площади плоских фигур: для прямоугольника (рис. 1.3, а)
длятреугольника (рис. 1.3, б)
|

 Сила - количественная мера механического взаимодействия материальных тел, характеризующаяся величиной, направлением и точкой приложения. Сила является векторной величиной. Прямая, по которой направлен вектор силы
Сила - количественная мера механического взаимодействия материальных тел, характеризующаяся величиной, направлением и точкой приложения. Сила является векторной величиной. Прямая, по которой направлен вектор силы  , называется линией действия силы (рис. 1.1).
, называется линией действия силы (рис. 1.1).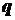 , то есть величиной силы, приходящейся на единицу длины. Заменим нагрузку, распределенную вдоль отрезка прямой по произвольному закону, сосредоточенной силой (рис. 1.2).
, то есть величиной силы, приходящейся на единицу длины. Заменим нагрузку, распределенную вдоль отрезка прямой по произвольному закону, сосредоточенной силой (рис. 1.2). Равнодействующей распределенной нагрузки будет сила
Равнодействующей распределенной нагрузки будет сила  , равная по модулю площади фигуры
, равная по модулю площади фигуры  , измеряемой в соответствующем масштабе. Линия действия силы
, измеряемой в соответствующем масштабе. Линия действия силы  (1.1)
(1.1)
 . (1.2)
. (1.2) Для прямоугольника линия действия силы
Для прямоугольника линия действия силы 


