Уравнения плоского движения.
Основная теорема Движение плоской фигуры в своей плоскости складывается из двух движений: поступательного вместе с произвольно выбранной точкой (полюсом), и вращательного вокруг этого полюса. Положение плоской фигуры на плоскости определяется положением выбранного полюса и углом поворота вокруг этого полюса, поэтому плоское движение описывается тремя уравнениями:
Первые два уравнения (рис.5) определяют то движение, которое фигура совершала бы при φ = const, очевидно, что это движение будет поступательным, при котором все точки фигуры будут двигаться так же, как полюс А. Третье уравнение определяет движение, которое фигура совершала бы при хА = const и уА = const, т.е. когда полюс А будет неподвижен; это движение будет вращением фигуры вокруг полюса А. При этом вращательное движение не зависит от выбора полюса, а поступательное движение характеризуется движением полюса.
Рассмотрим две точки А и В плоской фигуры. Положение точкиВ относительно неподвижной системы координат Оху определяется радиусом-вектором rB (рис.5): rB = rA + ρ;, где rA - радиус-вектор точки А, ρ = АВ вектор, определяющий положение точки В относительно подвижных осей Ах1у1, перемещающихся поступательно вместе с полюсом А параллельно неподвижным осям Оху. Тогда скорость точки В будет равна
В полученном равенстве величина Величина
Следовательно, Скорость любой точки В плоской фигуры равна геометрической сумме скорости VA выбранного полюса А и скорости VBA точки во вращательном движении вокруг полюса (рис.6):
Скорость вращательного движения
Модуль и направление скорости точки В находится построением соответствующего параллелограмма (рис.6).
|


 Зависимость между скоростями двух точек плоской фигуры.
Зависимость между скоростями двух точек плоской фигуры. .
. является скоростью полюса А.
является скоростью полюса А. равна скорости, которую точка В получает при
равна скорости, которую точка В получает при  = соnst, т.е. относительно осей Ах1у1 при вращении фигуры вокруг полюса А. Введем для этой скорости обозначение
= соnst, т.е. относительно осей Ах1у1 при вращении фигуры вокруг полюса А. Введем для этой скорости обозначение  :
: .
.
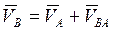

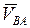 точки направлена перпендикулярно отрезку АВ и равна
точки направлена перпендикулярно отрезку АВ и равна




