Используя определение вектора ускорения (1.6) и формулу (2.1), получаем:

 (а)
(а)
Вычислим вектор  . Прежде всего, найдем направление этого вектора. Рассмотрим тождество
. Прежде всего, найдем направление этого вектора. Рассмотрим тождество

Дифференцируя это тождество по скалярному аргументу  , получаем:
, получаем:
 или
или 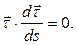
Но  в общем случае вектор
в общем случае вектор  изменяет со временем свое направление, так что
изменяет со временем свое направление, так что  Следовательно, скалярное произведение обратилось в нуль потому, что сомножители взаимно перпендикулярны.
Следовательно, скалярное произведение обратилось в нуль потому, что сомножители взаимно перпендикулярны.
Таким образом, вектор  перпендикулярен касательной, т.е. направлен по нормали к траектории. Ранее было показано, что вектор ускорения лежит в соприкасающейся плоскости. Следовательно, речь идет о главной нормали. Таким образом,
перпендикулярен касательной, т.е. направлен по нормали к траектории. Ранее было показано, что вектор ускорения лежит в соприкасающейся плоскости. Следовательно, речь идет о главной нормали. Таким образом,
 (б)
(б)
Остается вычислить
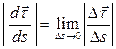
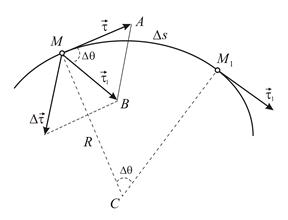 Пусть
Пусть  и
и  две близкие точки траектории. В точке
две близкие точки траектории. В точке  проведем главную нормаль
проведем главную нормаль  В точке
В точке  построим нормаль
построим нормаль  , пересекающую в точке
, пересекающую в точке  главную нормаль, построенную в точке
главную нормаль, построенную в точке  (если траектория плоская кривая, то
(если траектория плоская кривая, то 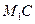 также будет главной нормалью). Угол между двумя близкими касательными, угол
также будет главной нормалью). Угол между двумя близкими касательными, угол  , называется углом смежности. В силу близости точек
, называется углом смежности. В силу близости точек  и
и  угол между нормалями
угол между нормалями  и
и 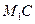 приближенно равен углу
приближенно равен углу  (для плоской кривой это равенство точное). В силу малости дугу
(для плоской кривой это равенство точное). В силу малости дугу 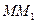 можно считать дугой окружности радиуса
можно считать дугой окружности радиуса  . Тогда
. Тогда  Из равнобедренного треугольника
Из равнобедренного треугольника  определяем
определяем
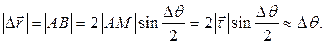
Тогда
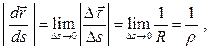
где  — предельное значение радиуса окружности, дуга которой в бесконечно малой окрестности точки
— предельное значение радиуса окружности, дуга которой в бесконечно малой окрестности точки  совпадает с дугой траектории. Эта окружность расположена в соприкасающейся плоскости, построенной для точки
совпадает с дугой траектории. Эта окружность расположена в соприкасающейся плоскости, построенной для точки  . Ее центр лежит на главной нормали и называется центром кривизны траектории в точке
. Ее центр лежит на главной нормали и называется центром кривизны траектории в точке  . Ее радиус
. Ее радиус  называется радиусом кривизны траектории в точке
называется радиусом кривизны траектории в точке  .
.
Окончательно получаем:

Совокупность приложенных к телу сил называется системой сил.


 (а)
(а) . Прежде всего, найдем направление этого вектора. Рассмотрим тождество
. Прежде всего, найдем направление этого вектора. Рассмотрим тождество
 , получаем:
, получаем: или
или 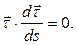
 в общем случае вектор
в общем случае вектор  изменяет со временем свое направление, так что
изменяет со временем свое направление, так что  Следовательно, скалярное произведение обратилось в нуль потому, что сомножители взаимно перпендикулярны.
Следовательно, скалярное произведение обратилось в нуль потому, что сомножители взаимно перпендикулярны. перпендикулярен касательной, т.е. направлен по нормали к траектории. Ранее было показано, что вектор ускорения лежит в соприкасающейся плоскости. Следовательно, речь идет о главной нормали. Таким образом,
перпендикулярен касательной, т.е. направлен по нормали к траектории. Ранее было показано, что вектор ускорения лежит в соприкасающейся плоскости. Следовательно, речь идет о главной нормали. Таким образом, (б)
(б)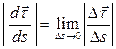
 Пусть
Пусть  и
и  две близкие точки траектории. В точке
две близкие точки траектории. В точке  В точке
В точке  , пересекающую в точке
, пересекающую в точке  главную нормаль, построенную в точке
главную нормаль, построенную в точке  , называется углом смежности. В силу близости точек
, называется углом смежности. В силу близости точек  и
и 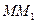 можно считать дугой окружности радиуса
можно считать дугой окружности радиуса  . Тогда
. Тогда  Из равнобедренного треугольника
Из равнобедренного треугольника  определяем
определяем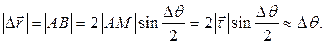
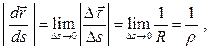
 — предельное значение радиуса окружности, дуга которой в бесконечно малой окрестности точки
— предельное значение радиуса окружности, дуга которой в бесконечно малой окрестности точки 



