Абсолютное и относительное движение точки. переносное движение .скорость точки при сложном движении
Направление полного ускорения определим по тангенсу угла α, который полное ускорение образует с нормальным ускорением (рис. 52). Получим tgα= tgα=
В ряде случаев приходится рассматривать движение точки по отношению к системе координат О1ξηζ, которая, в свою очередь, движется по отношению к другой системе координат Охуz условно принятой в качестве неподвижной. В механике каждую из указанных систем координат связывают с некоторым телом. Например, рассмотрим качение без скольжения колеса вагона по рельсу. С рельсом свяжем неподвижную систему координат Аху, а подвижную систему Oξη свяжем с центром колеса и предположим, что она движется поступательно. Движение точки на ободе колеса является составным или сложным. Введем следующие определения: Переносным движением точки называется ее движение в рассматриваемый момент времени вместе с подвижной системой координат относительно неподвижной системы координат. Переносная скорость и переносное ускорение точки обозначается индексом е: Переносной скоростью Проведем радиус-вектор начала координат
Чтобы найти переносную скорость точки в заданный момент времени необходимо продифференцировать радиус-вектор
Переносное ускорение соответственно равно
Таким образом для определения переносной скорости
Сложным движением точки называется такое ее движение, при котором она движется относительно системы отсчета, перемещающейся по отношению к некоторой другой системе отсчета, принятой за неподвижную. Например, можно считать, что пассажир, идущий по вагону движущегося поезда, совершает сложное движение по отношению к полотну дороги, состоящее из движения пассажира по отношению к вагону (подвижная система отсчета) и движения пассажира вместе с вагоном по отношению к полотну дороги (неподвижная система отсчета). Движение точки по отношению к подвижной системе координат называется относительным движением точки. Скорость и ускорение этого движения называют относительной скоростью и относительным ускорением и обозначают Движение точки, обусловленное движением подвижной системы координат, называется переносным движением точки. Переносной скоростью и переносным ускорением точкиназывают скорость и ускорение той, жестко связанной с подвижной системой координат точки, с которой совпадает в данный момент времени движущаяся точка, и обозначают Движение точки по отношению к неподвижной системе координат называется абсолютным или сложным. Скорость и ускорение точки в этом движении называют абсолютнойскоростью и абсолютным ускорением и обозначают В приведенном выше примере движение пассажира относительно вагона будет относительным, а скорость – относительной скоростью пассажира; движение вагона по отношению к полотну дороги будет для пассажира переносным движением, а скорость вагона, в котором находится пассажир, будет в этот момент его переносной скоростью; наконец, движение пассажира по отношению к полотну будет его абсолютным движением, а скорость – абсолютной скоростью.
§ 21. Определение скорости точки при сложном движении Пусть имеется неподвижная система отсчета
где неподвижной системы отсчета системы координат положение относительно подвижной системы координат.
где
При относительном движении координаты
где точки над величинами означают производные от этих величин по времени:
Если относительного движения нет, то точка
Выражение для абсолютной скорости найдем, дифференцируя по времени
В соответствии с формулами (2.70), (2.71) первая скобка в (2.72) есть переносная скорость точки, а вторая - относительная. Итак, Равенство (2.73) выражает теорему о сложении скоростей: абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей. Ответы по статике
|





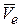 ,
,  .
. (ускорению
(ускорению  ) той точки m подвижной системы координат, с которой совпадает в данный момент движущая точка М (рис. 8.1).
) той точки m подвижной системы координат, с которой совпадает в данный момент движущая точка М (рис. 8.1). (рис. 8.1). Из рисунка видно, что
(рис. 8.1). Из рисунка видно, что . (8.4)
. (8.4)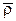 при условии, что координаты точки x, y, z не изменяются в данный момент времени:
при условии, что координаты точки x, y, z не изменяются в данный момент времени: . (8.5)
. (8.5) . (8.6)
. (8.6)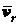 и
и  .
. и
и  .
.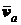 и
и  .
. по отношению к которой движется подвижная система отсчета
по отношению к которой движется подвижная система отсчета 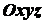 . Относительно подвижной системы координат движется точка
. Относительно подвижной системы координат движется точка  (рис. 2.26). Уравнение движения точки
(рис. 2.26). Уравнение движения точки  , (2.67)
, (2.67) - радиус-вектор точки
- радиус-вектор точки  - радиус-вектор, определяющий положение начала отсчета подвижной
- радиус-вектор, определяющий положение начала отсчета подвижной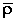 - радиус-вектор рассматриваемой точки
- радиус-вектор рассматриваемой точки  Пусть
Пусть 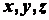 координаты точки
координаты точки  , (2.68)
, (2.68) - единичные векторы, направленные вдоль подвижных осей
- единичные векторы, направленные вдоль подвижных осей  . Подставляя (2.68) в равенство (2.67), получим:
. Подставляя (2.68) в равенство (2.67), получим: . (2.69)
. (2.69) по времени, учитывая его изменение только за счет относительного движения, то есть только за счет изменения координат
по времени, учитывая его изменение только за счет относительного движения, то есть только за счет изменения координат  , (2.70)
, (2.70) ,
,  ,
, 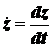 .
. . (2.71)
. (2.71) . (2.72)
. (2.72) . (2.73)
. (2.73)


