Касательное и нормальное ускорения точки . характер движения точки.
Касательное ускорение точки равно первой производной от модуля скорости или второй производной от расстояния по времени. Касательное ускорение обозначается –
Касательное ускорение в данной точке направлено по касательной к траектории движения точки; если движение ускоренное, то направление вектора касательного ускорения совпадает с направлением вектора скорости; если движение замедленное – то направление вектора касательного ускорения противоположно направлению вектора скорости. (рис. 8.5.)
Рис. 8.5
Нормальным ускорением точки называется величина, равная квадрату скорости, деленному на радиус кривизны. Вектор нормального ускорения направлен от данной точки к центру кривизны, (рис.8.6.). Нормальное ускорение обозначается
Рис. 8.6.
Полное ускорение точки
Рис. 8.7 Зная направление и модули
Характер — это такое исполнение движений, при котором у наблюдающих остается впечатление о легкости или грузности, округлости или угловатости, силе или расслабленности, свободе или скованности движений и т. п. Все эти оттенки создаются благодаря своеобразному подбору движений, осуществляющих действие 8.поступательное движения твердого тела. траектория, скорости и ускорения точек твердого тела при поступательном движении.
Поступательным движением твердого тела называется такое движение, при котором отрезок прямой, соединяющий две любые точки тела, во все время движения остается себе параллельным (например, АВ).
Теорема. При поступательном движении твердого тела траектории, скорости и ускорения всех его точек одинаковы.
Доказательство. Пусть отрезок АВ тела за время перемещается поступательно. Возьмем произвольную точку O и определим в пространстве положение отрезка АВ радиусами-векторами и. Обозначим: – радиус-вектор, определяющий положение точки В относительно точки А: . (1) Вектор не изменяется ни по величине, ни по направлению, так как (по определению поступательного движения). Из соотношения (1) видно, что траектория точки В получается из траектории точки А параллельным смещением точек этой траектории на постоянный вектор. Таким образом, траектории точек А и В будут одинаковыми. Возьмем производную по времени от равенства (1). Тогда , т.е.; или. Следовательно, при поступательном движении твердого тела скорости и ускорения всех его точек в данный момент времени одинаковы. Отметим, что сам факт поступательного движения не определяет ни закона движения, ни вида траектории. При поступательном движении точки тела могут описывать любые траектории (например, окружности). Но все они будут одинаковы. Дифференцируя левую и правую части приведенного выше векторного соотношения и учитывая, что dAB/dt=0, получаем drB/dt =drA/dt, или VB = VA. Дифференцируя по времени левую и правую части полученного соотношения для скоростей, находим dVB/dt=dVA/dt, или аB = аА. На основании вышеизложенного можно сделать следующий вывод: чтобы задать движение и определить кинематические характеристики тела, совершающего поступательное движение, достаточно задать движение одной его любой точки (по- Как и материальная точка, тело при его поступательном движении будет иметь одну степень свободы при движении по направляющей, задающей траекторию его точкам; две степени свободы в случае движения на плоскости (при постоянном контакте с ней хотя бы одной точкой) и три степени свободы в общем случае движения в пространстве.
9. вращения твердого тела вокруг неподвижной оси. Задания движения, угловая скорость и угловая ускорение, скорость и ускорения точек тела.
|

 .
. .
.
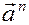 .
.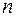 – нормаль к данной точке на траектории движения.
– нормаль к данной точке на траектории движения.

 определяется из векторного уравнения:
определяется из векторного уравнения:
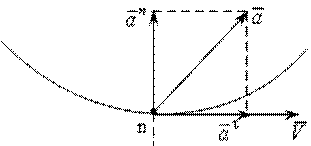
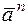 и
и  , по правилу параллелограмма определим ускорение, соответствующее данной точке траектории движения. Тогда модуль ускорения
, по правилу параллелограмма определим ускорение, соответствующее данной точке траектории движения. Тогда модуль ускорения  определим:
определим: .
.


