Теоретическая механика
Ответы по кинематике
Пусть точка  движется по траектории
движется по траектории 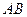 , на которой установлена криволинейная система отсчета (Рис.1.7).
, на которой установлена криволинейная система отсчета (Рис.1.7).
|
|
|
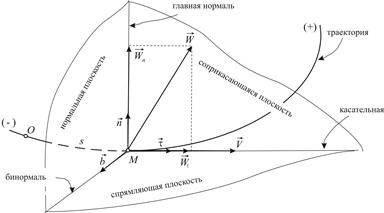
| Рис.1.7
|
|
|
В любой точке траектории существует единственная касательная. Обозначим  единичный вектор касательной; направлен
единичный вектор касательной; направлен  в сторону возрастания дуговой координаты. Нормаль, лежащая в соприкасающейся плоскости, называется главной нормалью. Обозначим
в сторону возрастания дуговой координаты. Нормаль, лежащая в соприкасающейся плоскости, называется главной нормалью. Обозначим  единичный вектор главной нормали;
единичный вектор главной нормали;  направлен в сторону вогнутости траектории. Нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью. Её единичный вектор
направлен в сторону вогнутости траектории. Нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью. Её единичный вектор 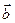 направлен так, чтобы векторы
направлен так, чтобы векторы 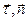 и
и 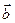 образовывали правую тройку.
образовывали правую тройку.
Соприкасающаяся, нормальная и спрямляющая плоскости образуют естественный трехгранник. Касательная, главная нормаль и бинормаль – оси естественного трехгранника; 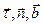 – орты этих осей.
– орты этих осей.
Оси естественного трехгранника играют существенную роль в описании движения точки, поскольку в этих осях вектор скорости и вектор ускорения вычисляются, как будет показано ниже, наиболее удобным образом. Пока отметим только, что разложение этих векторов по осям естественного трехгранника имеет вид:
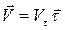 (1.8)
(1.8)
 (1.9)
(1.9)
где
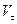 – проекция вектора скорости на направление касательной к траектории;
– проекция вектора скорости на направление касательной к траектории;
 – проекция вектора ускорения на направление касательной к траектории, которая называется касательным ускорением точки;
– проекция вектора ускорения на направление касательной к траектории, которая называется касательным ускорением точки;
 – проекция вектора ускорения точки на направление главной нормали к траектории точки, которая называется нормальным ускорением точки.
– проекция вектора ускорения точки на направление главной нормали к траектории точки, которая называется нормальным ускорением точки.
Оставляя доказательство для самостоятельного изучения, приведём окончательные результаты.
Для вектора скорости получаем:
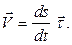 (1.10)
(1.10)
Таким образом,

 движется по траектории
движется по траектории 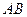 , на которой установлена криволинейная система отсчета (Рис.1.7).
, на которой установлена криволинейная система отсчета (Рис.1.7).
 единичный вектор касательной; направлен
единичный вектор касательной; направлен  единичный вектор главной нормали;
единичный вектор главной нормали; 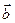 направлен так, чтобы векторы
направлен так, чтобы векторы 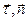 и
и 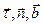 – орты этих осей.
– орты этих осей.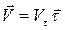 (1.8)
(1.8) (1.9)
(1.9)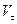 – проекция вектора скорости на направление касательной к траектории;
– проекция вектора скорости на направление касательной к траектории; – проекция вектора ускорения на направление касательной к траектории, которая называется касательным ускорением точки;
– проекция вектора ускорения на направление касательной к траектории, которая называется касательным ускорением точки; – проекция вектора ускорения точки на направление главной нормали к траектории точки, которая называется нормальным ускорением точки.
– проекция вектора ускорения точки на направление главной нормали к траектории точки, которая называется нормальным ускорением точки.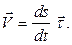 (1.10)
(1.10)


