Вращение твердого тела
Вращением твёрдого тела называется такой вид движения, при котором, по крайней мере, одна точка твёрдого тела остаётся неподвижной. Рассмотрим, однако, более простой случай – вращение АТТ вокруг неподвижной оси. Закрепим две точки АТТ: Ясно, что точки, не лежащие на оси вращения описывают окружности, центры которых лежат на оси вращения. Плоскости, в которых лежат такие окружности, перпендикулярны оси вращения. Следовательно: нам известны траектории всех точек тела. Это позволяет приступить к нахождению скорости любой точки твёрдого тела. При естественном способе задания движения точки:
Продифференцируем по времени полученное уравнения, учитывая, что величины R, S 0 и
Подставив (2.6) в (2.5) получим:
Эта формула неудобна, потому что сюда входит единичный вектор
Обозначим:
Ясно, что модуль Подставим (2.9) и (2.10) в (2.8):
Докажем, что
Направления
Угловая скорость – величина одинаковая для всех точек твердого тела. Линейная скорость любой точки твёрдого тела, вращающегося вокруг неподвижной оси, равна векторному произведению угловой скорости АТТ на радиус-вектор, проведённый из произвольной точки оси вращения, разложим
Сравнивая (2.15) и (2.14) получим: Модуль угловой скорости
При вращении тела его угловая скорость может изменяться, необходимо уметь определить угловую скорость тела в любой момент времени. Для этого введена величина, которая характеризует изменение угловой скорости с течением времени. Эту величину называют угловым ускорением. Дадим определение углового ускорения. Пусть в момент времени t угловая скорость
Для углового ускорения, его проекции на ось 0Z, модуля углового ускорения справедливы соотношения:
Перепишем выражение для ускорения точки:
Тангенциальное ускорение любой точки твёрдого тела, вращающегося вокруг неподвижной оси, равно векторному произведению углового ускорения тела на радиус – вектор этой точки, проведённой из произвольной точки оси вращения. 10.плоское движения твердого тела и движение плоской фигуры в ее плоскости.задания движения, независимость угловой скорости от выбора полюсов. 3.1 Определение. Примеры. Уравнения движения Плоскопараллельным (плоским) называется такое движение твёрдого тела, при котором все его точки перемещаются параллельно некоторой фиксированной плоскости. Плоские движения совершают многие части механизмов и машин, например:
А 2) шатун АВ в кривошипно- шатунном механизме О В
3) звено АВ в спарнике
О1 О2
Частным случаем плоскопараллельного движения является вращательное движение твёрдого тела вокруг неподвижной оси. Рассмотрим сечение S тела плоскостью OXY, параллельной неподвижной плоскости П (рисунок 3.1). При плоскопараллельном движении все точки тела, лежащие на прямой АВ, перпендикулярной сечению S, т.е. плоскости П, движутся тождественно.
S О Х
В Рисунок 3.1 Таким образом, для изучения движения всего тела достаточно изучить движение плоской фигуры S, поэтому в дальнейшем вместо плоского движения тела будем рассматривать движение плоской фигуры S в её плоскости, т.е в плоскости ОХУ. Положение плоской фигуры S в плоскости OXY определяется положением какого-нибудь проведённого на этой фигуре отрезка АВ (рисунок 3.2), а положение этого отрезка можно определить, зная координаты XA и YA точки А и угол j, который отрезок АВ образует с осью Х. Точку А, выбранную для определения положения фигуры S, называют полюсом.
yА
O xА x Рисунок 3.2 При движении фигуры величины ХА, УА, j будут изменяться. Чтобы знать закон движения фигуры S, т.е. её положение в любой момент времени в плоскости ОХУ, надо знать зависимости: xА=f1(t); yА=f2(t); j=f3(t). (3.1) Уравнения (3.1) являются уравнениями движения плоской фигуры в её плоскости или уравнениями плоскопараллельного движения тела. 3.2 Разложение плоского движения твёрдого тела на простые. Кинематические характеристики Рассмотрим движение плоской фигуры (рисунок 3.3); например два её положения – I и II, определяемые положениями отрезка АВ. Перемещение плоской фигуры из I в II можно заменить двумя простыми плоскими перемещениями - поступательным и вращательным, которые можно выполнять по отдельности или одновременно.
А А1 I II
Рисунок 3.3
Таким образом, плоскопараллельное движение фигуры представляет собой совокупность двух движений, происходящих одновременно: поступательного движения всех точек фигуры вместе с полюсом (например: точка А) и вращательного движения всех точек фигуры вокруг полюса. Исходя из уравнения (3.1) кинематическими характеристиками плоского движения являются скорость и ускорение поступательного движения, равные скорости и ускорению полюса ( Если за полюс выбрать любую другую точку фигуры, то кинематические характеристики поступательного движения изменяются, а кинематические характеристики вращательного движения останутся неизменными, т.е. вращательная часть плоского движения от выбора полюса не зависит. 3.3 Векторная формула для вычисления скоростей точек плоской фигуры В п. 3.2 было показано, что движение плоской фигуры можно рассматривать как слагающееся из поступательного движения, при котором все точки фигуры движутся со скоростью полюса – Va и из вращательного движения всех точек фигуры вокруг этого полюса. Покажем, что скорость любой точки В плоской фигуры складывается геометрически из скоростей, которые точка приобретает в каждом из этих движений. Рассмотрим плоскую фигуру, свяжем радиусами-векторами точки А и В этой фигуры с осями ОХУ:
VA
rB w
Рисунок 3.4
где VВА=wAB, (3.2 / )
Таким образом, скорость произвольной точки В плоской фигуры геометрически складывается из скорости какой-либо другой точки А, принятой за полюс, и скорости, которую точка В получает при вращении фигуры вокруг этого полюса; т.е.
В выражении (3.2) присутствуют кинематические характеристики как поступательного, так и вращательного движений, что ещё раз подчеркивает, что плоское движение – это сложное движение, являющееся совокупностью поступательного и вращательного движений. Модуль и направление Рассмотрим, например, колесо, катящееся по прямолинейному отрезку пути без скольжения; центр колеса точка С имеет скорость
Рисунок 3.5
Чтобы вычислить численные значения скоростей точек В и D, используют теорему косинусов, для чего необходимо знать углы между векторами 3.4 Векторная формула для вычисления ускорения точек плоской фигуры Покажем, что ускорение любой точки В плоской фигуры (так же как и скорость) складывается из ускорений, которые точка получает при поступательном и вращательном движениях этой фигуры. Рассмотрим плоскую фигуру с полюсом в точке А.
Рисунок 3.6
Продифференцируем дважды по времени (3.2) и получим:
или где или Таким образом, ускорение произвольной точки плоской фигуры В геометрически складывается из ускорения полюса Модуль и ускорение Однако вычисление Следует отметить, что
Если полюс А движется не прямолинейно, то его ускорение можно тоже представить как сумму касательной и нормальной составляющей, тогда можно записать:
Формулы 3.5–3.7 обычно используют при решении задач.
Рисунок 3.7 3.5 Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей (М.Ц.С) Другой более простой и наглядный метод определения скоростей точек тела при плоском движении основан на понятии о мгновенном центре скоростей. М.ц.с- это такая точка в плоскости плоской фигуры, скорость которой в данный момент времени равна нулю. Обозначают её Р. В данный момент времени это единственная точка, скорость, которой равна нулю. Способы определения м.ц.с: 1) если плоскопараллельное движение осуществляется путём качения без скольжения цилиндрического тела по какой-либо неподвижной поверхности, то точка соприкосновения катящегося тела с поверхностью имеет скорость, равную нулю, следовательно, является м.ц.с. Примером служит качение колеса по рельсу.
с
Плоское движение в полном соответствии с уравнениями представляет собой совокупность поступательного и вращательного движений, причем модель плоского движения тела можно рассматривать как поступательное движение всех точек тела вместе с полюсом и вращение тела относительно полюса.
2. Траектории поступательного движения тела зависят от выбора полюса. На рис. 13.3 в рассмотренном случае видим, что в первом способе движения, когда за полюс принимали точку
3. Вращение тела от выбора полюса не зависит. Угол
Основными характеристиками тела при плоском движении являются: траектория движения полюса, угол вращения тела вокруг полюса, скорость и ускорения полюса, угловая скорость и угловое ускорение тела. Дополнительные оси
Скорость полюса плоской фигуры можно определить с помощью производных по времени от уравнений:
Аналогично определяют угловые характеристики тела: угловую скорость
угловое ускорение
На рис. в полюсе А показаны проекции вектора скорости
Для сечения плоской фигуры точка А принята за полюс. Положение полюса определено радиусом-вектором Запишем векторное равенство
Вектор скорости точки М
В полученном уравнении
где
На рис. угловая скорость
11.определение скорости любой точки плоской фигуры путем сложения скорости полюса и скорости этой точки во вращательном движении плоской фигуры вокруг полюса (формула сложения скоростей). Теорема о проекции скоростей двух точек плоской фигуры.
|

 . Рассмотрим, как будут двигаться все точки твёрдого тела и научимся определять скорости и ускорения этих точек. Ясно, что точки твёрдого тела, лежащие на прямой, проходящей через две закреплённые точки, двигаться не будут: эту прямую называют неподвижной осью вращения. Движение твёрдого тела, при котором по крайней мере две его точки неподвижны, называют вращением АТТ вокруг неподвижной оси.
. Рассмотрим, как будут двигаться все точки твёрдого тела и научимся определять скорости и ускорения этих точек. Ясно, что точки твёрдого тела, лежащие на прямой, проходящей через две закреплённые точки, двигаться не будут: эту прямую называют неподвижной осью вращения. Движение твёрдого тела, при котором по крайней мере две его точки неподвижны, называют вращением АТТ вокруг неподвижной оси.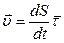 (2.5)
(2.5) Выберем неподвижную систему отсчёта, ось 0Z которой совпадает с осью вращения. Угол между неподвижной плоскостью X0Z, проходящей через ось вращения и плоскостью, жёстко связанной с твёрдым телом и проходящей через ось вращения, обозначим через
Выберем неподвижную систему отсчёта, ось 0Z которой совпадает с осью вращения. Угол между неподвижной плоскостью X0Z, проходящей через ось вращения и плоскостью, жёстко связанной с твёрдым телом и проходящей через ось вращения, обозначим через  . В начальный момент времени
. В начальный момент времени  . Рассмотрим движение точки М по окружности радиуса R.
. Рассмотрим движение точки М по окружности радиуса R. ;
;  ;
; 
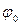 являются постоянными:
являются постоянными: (2.6)
(2.6) (2.7)
(2.7) , который зависит от положения точки. Мы привыкли положение точки задавать радиус-вектором
, который зависит от положения точки. Мы привыкли положение точки задавать радиус-вектором  . Он должен входить в формулу для скорости. Для этого проведём следующие преобразования: используя, что
. Он должен входить в формулу для скорости. Для этого проведём следующие преобразования: используя, что  , перепишем соотношение (2.7) в виде
, перепишем соотношение (2.7) в виде (2.8)
(2.8) – не зависит от выбора рассматриваемой точки М; (2.9)
– не зависит от выбора рассматриваемой точки М; (2.9) – вектор, проведенный из центра окружности к точке М. (2.10)
– вектор, проведенный из центра окружности к точке М. (2.10) равен радиусу окружности.
равен радиусу окружности. (2.11)
(2.11) (2.12)
(2.12)
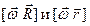 совпадают с направлением единичного вектора касания
совпадают с направлением единичного вектора касания  – линейная скорость точки М. (2.13)
– линейная скорость точки М. (2.13)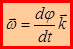 – угловая скорость. (2.14)
– угловая скорость. (2.14) по ортам:
по ортам: . (2.15)
. (2.15) ; модуль
; модуль  ; единица измерения
; единица измерения 
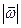 связан с частотой вращения
связан с частотой вращения  абсолютно твердого тела:
абсолютно твердого тела:
 . А в момент времени t+∆t угловая скорость равна
. А в момент времени t+∆t угловая скорость равна  . Составим отношение изменения угловой скорости к промежутку времени, в течение которого это изменение происходит, и найдём предел этого отношения при ∆t → 0. В механике этот предел называют угловым ускорением тела и обозначают
. Составим отношение изменения угловой скорости к промежутку времени, в течение которого это изменение происходит, и найдём предел этого отношения при ∆t → 0. В механике этот предел называют угловым ускорением тела и обозначают  поэтому:
поэтому:  . Угловое ускорение – величина одинаковая для всех точек твердого тела. Единицей измерения углового ускорения является
. Угловое ускорение – величина одинаковая для всех точек твердого тела. Единицей измерения углового ускорения является  . Используя (2.13) определим линейное ускорение точки М:
. Используя (2.13) определим линейное ускорение точки М: .
.
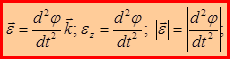
 (2.16)
(2.16) (2.17)
(2.17)

 1) катящееся колесо на прямолинейном участке пути:
1) катящееся колесо на прямолинейном участке пути:
 А В
А В А У
А У
 y В2 В1
y В2 В1

 0 x
0 x
 ), а также угловая скорость w и угловое ускорение x вращательного движения вокруг полюса.
), а также угловая скорость w и угловое ускорение x вращательного движения вокруг полюса.

 y
y 
 В
В 

 – радиус-вектор полюса А;
– радиус-вектор полюса А; – радиус-вектор произвольной точки В.
– радиус-вектор произвольной точки В. – вектор, определяющий положение точки В относительно осей AX1Y1, перемещающихся вместе с полюсом А поступательно.
– вектор, определяющий положение точки В относительно осей AX1Y1, перемещающихся вместе с полюсом А поступательно.  , т.к. фигура твёрдая, тогда
, т.к. фигура твёрдая, тогда  , продифференцировав по времени, получим
, продифференцировав по времени, получим или
или  , (3.2)
, (3.2) – это скорость, которую приобретает точка В при вращении фигуры вокруг полюса А, поэтому
– это скорость, которую приобретает точка В при вращении фигуры вокруг полюса А, поэтому , где w – угловая скорость фигуры.
, где w – угловая скорость фигуры. . (3.3)
. (3.3) определяются построением соответствующего параллелограмма (рисунок 3.5).
определяются построением соответствующего параллелограмма (рисунок 3.5). . Выберем две произвольные точки В и D на ободе колеса и, используя выражение (3.3), запишем их скорости:
. Выберем две произвольные точки В и D на ободе колеса и, используя выражение (3.3), запишем их скорости:
 ;
;  ;
;
 . (3.4)
. (3.4) и
и  ;
;  и
и  .
.
 или
или 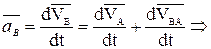
 (3.5)
(3.5) ,
,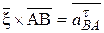 ;
;  ; (3.6)
; (3.6) (3.5 /)
(3.5 /) и ускорения, которое точка В получает при вращении фигуры вокруг этого полюса.
и ускорения, которое точка В получает при вращении фигуры вокруг этого полюса. находятся построением соответствующего параллелограмма (рисунок 3.6).
находятся построением соответствующего параллелограмма (рисунок 3.6).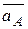 и
и  , поэтому
, поэтому  удобнее заменять его касательной (
удобнее заменять его касательной ( ) и нормальной (
) и нормальной ( ) составляющими, (3.6).
) составляющими, (3.6).
 , а
, а 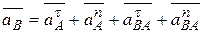 (3.7)
(3.7)
 w
w
 ,траектория поступательного движения
,траектория поступательного движения  значительно отличается от траектории
значительно отличается от траектории  для другого полюса В.
для другого полюса В. вращения тела остается постоянным по модулю и направлению вращения. В обоих случаях, рассмотренных на рис. 13.3, вращение произошло против вращения часовой стрелки.
вращения тела остается постоянным по модулю и направлению вращения. В обоих случаях, рассмотренных на рис. 13.3, вращение произошло против вращения часовой стрелки. при поступательном движении перемещаются вместе с полюсом А параллельно основным осям Оху по траектории движения полюса.
при поступательном движении перемещаются вместе с полюсом А параллельно основным осям Оху по траектории движения полюса.

 ;
; .
.
 на оси Ох,Оу. Угол вращения тела
на оси Ох,Оу. Угол вращения тела  и угловое ускорение
и угловое ускорение  показаны дуговыми стрелками вокруг точки А. В связи с независимостью вращательных характеристик движения от выбора полюса угловые характеристики
показаны дуговыми стрелками вокруг точки А. В связи с независимостью вращательных характеристик движения от выбора полюса угловые характеристики  , проведённым из начала координат в точку А. Требуется установить связь скорости точки М тела с характеристиками плоского движения тела. Отрезок
, проведённым из начала координат в точку А. Требуется установить связь скорости точки М тела с характеристиками плоского движения тела. Отрезок  постоянной длины рассматривается как вектор, определяющий положение точки М относительно полюса А.
постоянной длины рассматривается как вектор, определяющий положение точки М относительно полюса А.
 , где
, где  - радиус-вектор полюса А;
- радиус-вектор полюса А;  - радиус-вектор, определяющий положение точки М относительно полюса А.
- радиус-вектор, определяющий положение точки М относительно полюса А. или
или  .
. - скорость точки М, которую она получает при вращении телавокруг полюса А:
- скорость точки М, которую она получает при вращении телавокруг полюса А: или
или 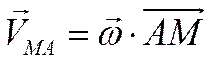 ,
, - вектор угловой скорости тела.
- вектор угловой скорости тела.




