Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.
13. а) Если сила F постоянна во времени и ее направление совпадает с направлением перемещения тела, то работа W находится по формуле.
Здесь: б) А тяж (работа силы тяжести) = mg(h2 - h1) в) А упр = k умножить на дельта (треугольничек) l1 в квадрате и разделить на два минус k*дельта l2в квадрате разделить на два 14. 1) Работа внешних сил равна взятой с обратным знаком работе внутренних сил:
15. 1) Дифференциальные уравнения поступательного движения твердого тела: Дифференциальные уравнения вращения твердого тела вокруг неподвижной оси: Jz – момент инерции тела относительно оси вращения z, 2) Jz ⋅ dω/dt = Mвращ, или Jz ⋅ d 2 φ /dt 2 =Mвращ. (3.13)
Уравнение (3.13) представляет собой дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси. 3)
где Уравнения (3) представляют собой дифференциальные уравнения плоскопараллельного движения твердого тела 16.
|
.
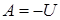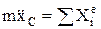и т.д. 
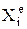– проекция внешней силы. Все точки тела движутся так же, как и его центр масс С. Для осуществления поступательного движения необходимо, чтобы главный момент всех внешних сил относительно центра масс был равен 0: 
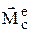=0.
,
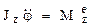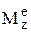– момент внешних сил относительно оси вращения (вращающий момент). 
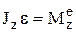, e – угловое ускорение, чем больше момент инерции при данном 
.
,
,
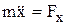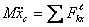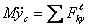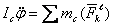
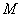- масса тела; 
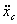и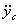 
-проекции ускорения центра масс на координатные оси.
