Интегральный метод факторного анализа
Чтобы избавится от серьезного недостатка, присущего индексному методу, методу цепных подстановок и всем их модификациям, применяется интегральный метод факторного анализа. Этот метод базируется на предположении, что результативный показатель представляет собой функцию от факторов. Значения функций при изменениях аргументов рассчитывается с помощью интегралов. Достоинство интегрального метода в том, что факторы находятся в равноправном положении и результаты расчетов не зависят от того, с какого фактора мы их начинаем. При интегральном методе факторного анализа мы получаем однозначный результат (без вариантов). Вместе с тем, интегральный метод имеет серьезный недостаток: с увеличением числа факторов сомножителей резко усложняются расчеты, т.к. увеличивается число возможных перестановок факторов. При проведении факторного анализа интегральный метод может быть использован для решения задач по двум направлениям. К первому направлению относится решение таких задач анализа, когда отсутствует информация об изменении факторов внутри анализируемого периода, или от этого изменения можно абстрагироваться. В данном случае величина изменения результативного показателя не зависит от порядка расположения факторов в модели. Этот тип задач называется статическим. В качестве примера можно привести сравнительный анализ показателей двух аналогичных объектов. Второе направление характеризуется задачами динамического типа, т.е. когда имеются данные об изменении факторов внутри анализируемого периода. Расчеты связаны с анализом временных рядов показателей. Интегральный метод факторного анализа дает общий подход к решению задач разного типа независимо от количества факторов, входящих в модель, схемы взаимосвязи между ними и порядка расположения факторов в модели. Этот метод позволяет осуществить расчеты влияния факторов на результативный показатель в мультипликативных, кратных и смешанных моделях без образования «неразложимого остатка». Рассмотрим использование интегрального метода на примере анализа выручки от продаж с помощью двухфакторной мультипликативной модели. Рассмотрим алгоритм расчетов влияния факторов интегральным методом для решения двухфакторной мультипликативной модели. Для расчета влияния факторов на изменение результативного показателя (выручки) используем интегральный метод, при котором изменение выручки можно представить как сумму двух интегралов. Один из них характеризует зависимость изменения выручки от количества проданного товара, а второй – зависимость выручки от цены единицы товара. Базовый вариант: B0 = q0 × p0 Отчетный вариант: B1 = q1 × p1 ∆B = B1 - B0 = где:
Исходя из предположения, что данные факторы в пределах небольшого промежутка времени изменяются по линейному закону, расчеты влияния факторов на изменение выручки можно представить следующим образом: 1) влияние изменения количества проданного товара ∆B(q) = ∆q × p0 + 2) влияние изменения цены единицы товара
Проверка: ∆B = B1 - B0 = ∆B(q) + ∆B(p) (20)
В практике аналитической работы интегральный метод не получил широкого распространения. Он используется преимущественно в научно-исследовательских разработках в области экономического анализа. Далее рассмотрим основные методы и приемы расчета влияния факторов в различных типах зависимостей. Выбор метода расчета влияния факторов определяется его достоинствами и недостатками перед остальными в каждой конкретной ситуации. Характеристики детерминированного факторного анализа приведены в Таблице 5. Таблица 5. Характеристика методов детерминированного факторного анализа
|

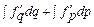 ,
,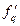 - функция изменения выручки в зависимости от количества проданного товара;
- функция изменения выручки в зависимости от количества проданного товара;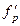 - функция изменения выручки в зависимости от цены единицы товара.
- функция изменения выручки в зависимости от цены единицы товара.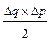 (18)
(18)


