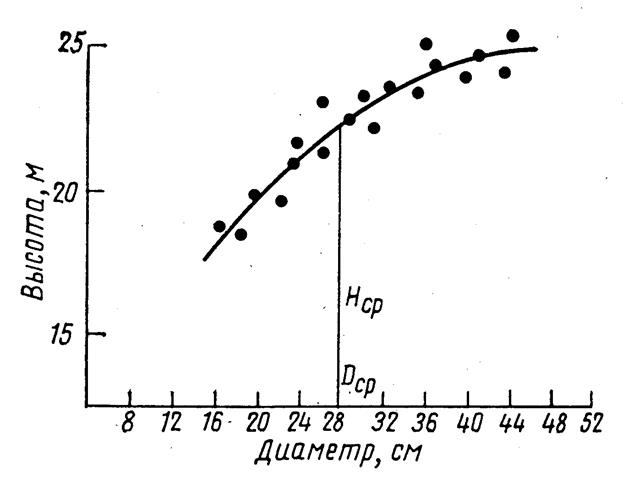
Средняя высота насаждений
Высота деревьев в любом насаждении не одинакова. В пределах насаждения различия в высоте наблюдаются не только у деревьев разной толщины, но они имеют место и у деревьев равных диаметров. В процессе таксации леса учесть индивидуальную высоту каждого дерева не представляется возможным. В связи с этим принято устанавливать среднюю высоту для всей совокупности деревьев, образующих насаждение. Средняя высота насаждений зависит от древесной породы, условий местопроизрастания, возраста и осуществляемых в лесу хозяйственных мероприятий. В пределах насаждения различия в высоте обусловливаются разным положением деревьев в отношении света, смежных деревьев, микроповышений и почвенных разностей. Влияние перечисленных факторов на высоту деревьев не имеет количественно выраженных зависимостей, и их установление представляет трудную задачу. При одном и том же диаметре деревьев в пределах насаждения высоты оказываются разными. Из-за конкуренции за свет распределение деревьев по высоте показывает положительную асимметрию. Однако стохастические связи между h и d позволяют строить кривые высот на основе небольшого количества измерений, но дающих достаточно точные оценки высот для практических и научных целей Профессором Лореем более 100 лет назад предложена следующая формула для определгния средней высоты насаждения: hL = hL - средняя высота; h1... hn - высота для отдельных ступеней толщины; g1... gn - площади сечения деревьев каждой ступени толщины. Большинство современных учёных считают среднею высоту, вычисленную по формуле Лорея, абстракцией, ничего в насаждении не выражающей. Средние таксационные показатели нам нужны чаще всего для нахождения запаса. Средняя высота, найденная по формуле Лорея, не всегда будет соответствовать среднему дереву по диаметру. Если же мы в качестве средней высоты возьмём высоту среднего дерева по диаметру, то в результате получим среднее дерево по объёму, учитывая высокую корреляционную зависимость высоты и видового числа. Поэтому наиболее корректно определять среднюю высоту по уравнениям связи между диаметрами и высотами. В этом случае среднюю высоту можно найти графически, путем построения кривой высот (рисунок 9.1). С этой целью обмеряют диаметры и высотs у ряда деревьев, отобранных тем или иным способом Результаты этих обмеров наносят на график, который строится в прямоугольных координатах. Если на графике взять длину перпендикуляра, восстановленного из точки, соответствующей среднему диаметру насаждения, то эта длина будет определять среднюю высоту всего насаждения. При построении кривых высот рекомендуется вычислять на основе обмеренных высот средние высоты по ступеням толщины и проводить плавную кривую через средние значения. . Пользуясь кривой высот, можно найти высоту деревьев любого диаметра. Для этого из точки на оси абсцисс, соответствующей диаметру данного дерева, надо восставить перпендикуляр до пересечения с кривой высот. Длина этого перпендикуляра (ординаты) является искомой высотой дерева. В более или менее однородных насаждениях наблюдается стохастическая (вероятностная) зависимость высоты деревьев от их диаметров. С увеличением последних у большинства деревьев соответственно растет и высота. Гогенадль, Кренн и другие исследователи связь между d1,3 и h в насаждении характеризуют уравнением параболы второго порядка. В настоящее время исследованием многих отечественных и зарубежных ученых установлено, что парабола 2-го порядка плохо описывает зависимость H-D. Она занижает значение высот в начале ряда и завышает их в конце. Для характеристики связи высоты и диаметра применяются более сложные кривые. Исследованиями К.Е.Никитина Ф.Корсуня, А.Г.Мошкалёва, Ф.П.Моисеенко установлено, что уравнения связи Н = f (Д) описываются разными уравнениями: полиномы от 3 до 4 степени, логарифмические кривые (простые и сложные), степенные и показательные функции. Среднюю высоту можно найти и как среднеарифметическую величину. Но это будет чисто статистическая величина. Она не характеризует среднее дерево по диаметру и запасу.
Рисунок 9.1. Определение средней высоты насаждения по кривой высот
Аналогично среднему диаметру можем найти высоту срединного дерева (hw), высоту средних ступеней толщины (hg m) и т.д. В этом ряду наименьшее значение будет иметь средняя арифметическая высота, а наибольшей будет высота, вычисленная по формуле Лорея. При отводе и таксации лесосек с использованием разрядных таблиц среднюю высоту для нахождения разряда высот определяют, измеряя 9 деревьев: 3 из центральной ступени толщины и по 3 из соседних. Варьирование высот в приспевающих и спелых древостоях составляет 6-8%. Следовательно, измеряя 12-15 деревьев мы определим Hср с точностью около 2%, а при 9 замерах 2-3%. В разновозрастных, многоярусных древостоях Hср находят для каждого яруса. В смешанном древостое измерения делают для каждой породы. Опытный таксатор после ежегодно проводимых тренировок среднюю высоту определяет глазомерно.. Средняя высота, определяемая как по формуле Лорея так и по графику высот, как таксационный показатель имеет недостаток, заключающийся в том, что на ее величину оказывает влияние вырубка части деревьев при уходе за лесом. Если этот уход ведется низовым способом, заключающимся в изъятии из насаждения отставших в росте более мелких деревьев, то средняя высота насаждения после ухода за ним увеличивается. При проведении верхового способа ухода за лесом вырубаются более крупные деревья. Соответственно этому обстоятельству после проведения таких рубок средняя высота насаждения уменьшается.
|

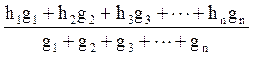 , где
, где