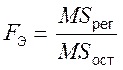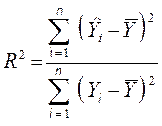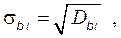Результатов опытов
Комплексным статистическим анализом экспериментальных данных предусматривается решение не только основной задачи исследования, например, как это было показано в лабораторных работах №1 (определение численного значения коэффициента корреляции r xy) и №2 (определение численных значений коэффициентов уравнения регрессии) с контролем статистической значимости полученных результатов и проверкой их адекватности. Однако получить аналогичные результаты анализа можно с использованием единой программы, позволяющей выполнить не только необходимые вычисления, но и графически отобразить их средствами компьютерной графики в заданном масштабе, а главное – обеспечить удобство изменения вида искомого уравнения регрессии. Остановимся здесь на некоторых положениях, имеющих принципиально важное значение. Закономерная изменчивость обусловлена причинно - следственными связями между выходом и входами объекта. Последние, в свою очередь, обладают случайной изменчивостью вследствие колебаний химического состава и свойств сырых материалов, напряжения в сетях электропитания, давления сжатого воздуха в заводских магистралях и пр. К случайной изменчивости относят также воздействие на выход объекта каких - либо факторов, неизвестных или ещё не выявленных на данной стадии исследования. Кроме того, определённая случайная изменчивость свойственна как входам, так и выходам объекта по причине случайных погрешностей их измерения. Встроенный математический аппарат электронных таблиц Excel позволяет выполнить статистический анализ данных, включая элементы регрессионного, корреляционного и дисперсионного анализа, не прибегая к программированию этой задачи. Последняя для своего решения требует лишь записи исходных данных в особой форме и дальнейшего манипулирования средствами Excel. Пусть в простейшем случае имеем линейное уравнение регрессии
Ŷ = b 0 + b 1 x 1 + b 2 x 2 + b 3 x 3 + … + bKxK,
n - общее количество отсчётов (опытов); Ŷi - соответствующее модельное значение выхода объекта. Значение n не должно быть меньше своего предельного минимума
n min = 2 + (K + 2)(K +1) / 2.
При регрессионном анализе используются такие понятия, как регрессионная сумма квадратов, иначе - сумма квадратов, обусловленная регрессией
остаточная сумма квадратов (сумма квадратов ошибки регрессии)
SS ост =
- общая сумма квадратов
S yy = SS рег + SS ост =
В этих выражениях
Если ввести математические ожидания указанных сумм квадратов
MS рег = SS рег / f рег; MS ост = SS ост / f ост ,
где символом f обозначены соответствующие (известные из математики) числа степеней свободы
f рег = K; f ост = n – (K + 1); f yy = n – 1,
то отношение
является экспериментальным значением критерия Фишера, а величина
представляет собой квадрат множественного коэффициента корреляции (реже называется множественным коэффициентом детерминации). Величина F Э характеризует степень адекватности полученной математической модели, т. е. соответствия её исходным опытным данным, полученным от исследуемого объекта. При прямой оценке адекватности задаются требуемой доверительной вероятностью и по данным, например, [23, 34] из специальных таблиц выбирают теоретическое (табличное) значение критерия Фишера F T. При условии
F Э £ F T (*)
модель можно считать адекватной и наоборот. Возможна и обратная оценка, при которой по значению F Э непосредственно вычисляют доверительную вероятность, т.е. степень надёжности найденной математической модели. Критерий R 2 характеризует степень тесноты связи между рассматриваемыми переменными. Вообще,
0 £ R 2£ 1.
При R 2 = 0 закономерная связь между входами и выходом, выражаемая уравнением регрессии, отсутствует, а при R 2 = 1 эта связь становится функциональной - без случайной изменчивости данных и, следовательно, без разброса отдельных результатов отсчётов относительно линии или поверхности (гиперповерхности) регрессии в графическом представлении. Принято [410], ч.1, с. 80334 считать допустимым
R 2 ³ 0,7
В то же время, критерий F Э позволяет оценить доверительную вероятность вычисленного значения R 2 , что важно для учёта влияния на эту величину определённой изменчивости экспериментальных данных в формуле (*). Проверке подвергают также коэффициенты b i математической модели. Обычно это делается с применением критерия Стьюдента (это псевдоним Госсета - английского математика начала ХХ – го века). Экспериментальное значение данного критерия
где σ bi - стандартная (среднеквадратичная) ошибка определения коэффициента b iсогласно формуле
в которой D b i - дисперсия тех данных, по которым определён этот коэффициент. При прямом подходе к оценке значимости коэффициентов математической модели [23], [45] задаются необходимой для решаемой задачи доверительной вероятностью и по ней выбирают теоретическое (табличное) значение критерия Стьюдента t T. При условии
| b i | ³ t T. | s b i |
коэффициент bi считается значимым. В противном случае его обнуляют. Возможен и обратный подход, при котором непосредственно по рассчитанному значению t Э вычисляют доверительную вероятность для данного коэффициента bi. Далее, в зависимости от требований к проводимому исследованию, принимают решение сохранить данный коэффициент (и соответствующий член уравнения математической модели) или - принять его за нуль (“нуль - гипотеза”). Все рассмотренные и некоторые другие расчёты можно выполнить с использованием встроенного математического аппарата Excel. Для решения задачи следует записать исходные данные по специальной схеме, овладеть несложными приёмами манипулирования имеющимися средствами Excel и интерпретировать выдаваемые компьютером результаты. При этом необходимо следующее пояснение. Обычно в литературе приняты обозначения: a - уровень значимости ошибки определения той или иной величины при статистическом анализе, b = 1 - a - доверительная вероятность результатов определения этой величины. Разработчики Excel (фирма Microsoft) приняли иные обозначения, а именно: - уровень значимости ошибки определения экспериментального значения критерия Фишера F = F Э обозначен как “значимость F”, - критерий Стьюдента tЭ характеризуется как “ t - статистика”, - уровень значимости ошибки определения коэффициентов bi математической модели назван “P - значением”. Ознакомимся с приёмами использования Excel на конкретном примере. Пример.Пусть требуется оценить зависимость цены литейной продукции (Y) от производительности технологического процесса (x 1) и сводного показателя её качества (x 2) Используем в качестве примера данные [410], представленные в табл.6. Заполняем таблицу этими данными и сохраняем её для дальнейшего использования. Для решения задачи из главного меню запущенной в работу системы электронных таблиц Excel вводим команды
СЕРВИС | АНАЛИЗ ДАННЫХ | РЕГРЕССИЯ Ход решения заключается в том, что в окне “Регрессия” указываем входной диапазон значений Y в виде C2:C13, а общий входной диапазон значений аргументов (координаты левого верхнего и правого нижнего углов блока данных) A2:B13. Таблица 2
|

 в котором коэффициенты bi; i = 0, K средствами Excel определяются по методу наименьших квадратов. Сущность этого метода заключается в том, чтобы коэффициенты удовлетворяли условию
в котором коэффициенты bi; i = 0, K средствами Excel определяются по методу наименьших квадратов. Сущность этого метода заключается в том, чтобы коэффициенты удовлетворяли условию
 где i - номер отсчёта экспериментального значения выхода объекта Yi; i = 1, n;
где i - номер отсчёта экспериментального значения выхода объекта Yi; i = 1, n;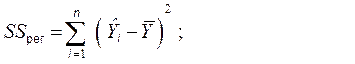

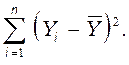
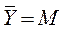 - среднее арифметическое значение выхода
- среднее арифметическое значение выхода