Задание на курсовую работу
Задание может быть типовым или индивидуальным. Типовым зада-нием предусмотрена комплексная обработка и анализ результатов полного факторного эксперимента (ПФЭ) с построением математической модели исследуемого объекта и оценкой её коэффициентов, а также адекватности модели по статистическим критериям. Вариант типового задания студент выбирает по своему шифру (см. далее табл.10 … 12). Индивидуальное задание руководитель назначает по желанию студента с учетом его производственного или научно-исследовательского опыта. Ниже приведены примеры индивидуальных заданий также по комплексной обработке и анализу результатов не только ПФЭ, но и дробных факторных экспериментов (ДФЭ), а также – регрессионно - корреляционного анализа данных пассивного эксперимента. Общие указания: по данным эксперимента студент строит математическую модель исследуемого объекта сначала как функцию кодированных (безразмерных) значений факторов X1, X2, X3 … [1, 2], а затем преобразует эту модель к виду функции натуральных (то есть имеющих конкретные размерности) значений тех же факторов x 1, x 2, x 3 …. При этом имеет место известное из теоретических основ дисциплины соотношение
где i - порядковый номер фактора, x oi – основной уровень фактора, в качестве которого часто принимают среднее арифметическое между верхним
Δ x i – интервал варьирования данного фактора. Отсюда Тогда математическая модель представляется в следующих видах:
где коэффициенты При x i = x 0i имеем Следует отметить, что натуральные x 1, x 2 и другие факторы в выражении математической модели исследуемого объекта на практике, то есть за пределами планируемого эксперимента, могут иметь произвольные значения как ниже, так и выше своих основных уровней, принятых при ПФЭ или ДФЭ. Это практически может быть использовано для прогнозирования поведения объекта, например, при совершенствовании технологических процессов. Однако необходимо иметь в виду, что надёжность такого прогноза сохраняется полной при условии, что значения факторов не выходят за пределы их варьирования, то есть имеет место интерполирование x i. При выходе же за пределы варьирования факторов (экстраполироование x i) степень адекватности модели может постепенно снижаться из – за нелинейности свойств объекта, и требуется выборочная проверка адекватности прогноза опытным путём. При обработке и анализе результатов пассивного эксперимента (вариант индивидуального задания) кодирования факторов не требуется, и математическую модель объекта строят по данным их случайных значений, полученных при различных неуправляемых воздействиях на объект и наличии погрешностей измерений. Исходные данные для выполнения типового задания следующие.
( По такому плану исследовалось, например, влияние трёх факторов: x 1 - содержания жидкого стекла (% от массы кварцевого песка); x 2 – количества феррохромового шлака (% от массы кварцевого песка), используемого в качестве отвердителя жидкого стекла, и x 3 – влажности этого шлака (%) на её сопротивлению разрыву y, Па, после отверждения в течение одного часа [21, 23]. Такая смесь используется в качестве облицовочной для изготовления тяжелых стальных отливок (уплотнение пескомётным способом). Содержание глины в количестве 1% остаётсяпостоянным. Приняты определённые значения верхних и нижних уровней варьируемых факторов и интервалов их варьирования, %: Таблица 12
Изменения результатов параллельных опытов при одних и тех же значениях факторов могут быть объяснены как непостоянством свойств кварцевого песка, используемого в разные периоды времени, так и погрешностями соответствующих измерений. Предварительные значения откликов студент выбирает из табл.13 в зависимости от предпоследней цифры своего шифра. Здесь в первой графе каждого столбца приведены результаты первого из двух параллельных опытов y u1, а во второй – второго, то есть y u2. Эти данные следует скорректировать по последней цифре шифра студента, согласно данным табл.14. Для этого исходные значения y uq алгебраически суммируют с поправкой.
Таблица 13
Продолжение табл. 13
Таблица 14
Например, студент, шифр которого оканчивается цифрами 82, для решения задачи принимает следующие данные (табл.19) результатов опытов (где - 0,5 является поправкой). Таблица 15
Требуется найти математическую модель исследуемого объекта при доверительной вероятности 0,95. Проверить однородность построчных дисперсий, оценить значимость отдельных коэффициентов и адекватность модели в целом. Охарактеризовать эффекты взаимодействия факторов, если они значимы. Выявить самый сильный и самый слабый факторы и указать направления их воздействия на отклик объекта. В случае признания математической модели неадекватной описать возможный план дальнейших действий исследователя, направленных на достижение адекватности искомой модели в реальной ситуации научного исследования.
Примеры индивидуальных заданий:
1) Исследуется процесс образования пригара на поверхности отливок из серого чугуна в сырых песчано – глинистых формах в зависимости от следующих факторов: - твёрдость формы x 1, варьируемая от нижнего уровня 70 до верхнего 90 ед.; - количество противопригарной добавки (каменноугольной пыли) x 2 соответственно от 0,5 до 1,5 % от массы песка; - температура заливки x 3, - от 1320 до 1360 °C. В качестве отклика y рассматривалась относительная поверхность отливки, поражённая пригаром, %. С целью выявления характера влияния рассматриваемых факторов на величину y реализован ПФЭ типа 23 , в котором кодированные значения факторов соответствуют данным табл.16. При этом каждый из 1 … 8 опытов поставлен дважды. Полученные значения отклика y 1 и y 2, %, представлены в той же табл. 16 Таблица 16
Требуется найти и описать математическую модель влияния данных факторов на степень развития пригара. Охарактеризовать влияние отдельных факторов (силу и направление воздействия) на процесс образования пригара. Рекомендации. Для выполнения задания использовать методику, во многом аналогичную используемой в типовом задании, с дополнительным обращением к литературе [12, …, 45]. 2) С целью установления зависимости прочности на сжатие (y 1, МПа) во влажном состоянии и текучести (y 2, %) песчано – глинистой формовочной смеси от изменения содержания в ней глины (x 1, %) и воды (х 2, %) при постоянном времени перемешивания в бегунах, равном 10 мин, поставлен полный факторный эксперимент (ПФЭ), матрица планирования которого типа 22 представлена в табл.17. Верхние уровни варьирования факторов х 1 и х 2 составили 12,0 и 5,5 %, нижние соответственно 8,0 и 3,5 %. Результаты исследования прочности смеси в двух сериях параллельных опытов обозначены как y '1 и y "1, а текучести – как y '2 и y "2. В той же таблице представлены построчные средние значения откликов y 1ср и y 2ср соответственно. Таблица 17
Найти и охарактеризовать искомую зависимость в виде математической модели в кодированных и натуральных значениях факторов. Рекомендации. Методика обработки и анализа результатов ПФЭ изложена в литературе [12, 23], особенности компьютерной обработки и анализа данных – в [34, 45]. 3) Исследованию подвергается песчано – глинистая формовочная смесь для формовки по - сырому, в составе которой варьируются в процентах от массы сухого кварцевого песка: - глина (фактор x 1) от нижнего уровня 8,0 до верхнего уровня 12,0 %; - вода (фактор x 2) соответственно от 3, 5 до 5,5 %; - продолжительность перемешивания компонентов в бегунах (фактор x 3) поддерживается равной 10 мин на нижнем уровне и 16 мин на верхнем. Требуется определить зависимость прочности формовочной смеси на сжатие y, МПа, от названных технологических факторов. Эту зависимость представить в виде математической модели, выраженной как в кодированных, так и в натуральных значениях факторов.
Таблица 18
Рекомендации. Для решения задачи необходимо использовать результаты y 1 и y 2 реализации каждого из двух параллельных опытов, МПа, в составе дробного факторного эксперимента (ДФЭ) типа 23-1, представленные в табл.18. На базе последних построить и охарактеризовать математическую модель исследуемой формовочной смеси, как функцию определяющих её факторов c использованием материалов [12 … 43]. 4) При пассивном эксперименте получена выборка (табл.19) – пассивный эксперимент - результатов контроля технологического процесса выплавки стали для изготовления отливок ответственного назначения, где исследуемыми факторами являются х 1 – температура металла в заключительном периоде плавки, °С; х 2 – основность шлака
как функция содержания в нём соответствующих компонентов, %; х 3 – содержание FeO в шлаке, %. Необходимо найти зависимость степени десульфурации стали
где [S]нач и [S]кон – начальное и конечное содержания серы в металле, %, от определяющих её факторов. Искомую зависимость представить в виде линейной математической модели, выраженной в натуральных значениях факторов. Эффекты взаимодействия факторов в рассматриваемой системе отсутствуют. Рекомендации. Для решения поставленной задачи наиболее целесообразно использовать табличный процессор Excel (функцию “Регрессия” в меню “Анализ данных”). При этом оценить значимость отдельных коэффициентов при доверительной вероятности 0,95, а адекватность модели проверить по критерию “R – квадрат”.
Таблица 19
5) Испытания образцов специального сплава при непостоянстве содержания в нём x 1 = [Si],% и x 2 = [Mn],% на фоне относительного постоянства концентраций других элементов (табл.20) при пассивном эксперименте показали существенный разброс прочности на растяжение y = σв, МПа. Необходимо найти зависимость прочности сплава от содержания в нём кремния и марганца в виде математической модели.
Оценить значимость коэффициентов и адекватность модели при доверительной вероятности 0,95. Охарактеризовать влияние рассматриваемых элементов на прочность сплава.
Таблица 20
Выявить наличие, вид и координаты [Si], [Mn], %, экстремума функции
|



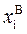 и нижним
и нижним  его натуральными значениями или одно из лучших значений, известных ко времени начала исследования
его натуральными значениями или одно из лучших значений, известных ко времени начала исследования

 ;
;
 остальные – по аналогии.
остальные – по аналогии. = a 0 = b 0 .
= a 0 = b 0 . Дана матрица планирования полного факторного эксперимента
Дана матрица планирования полного факторного эксперимента (табл.9) типа 23, где
(табл.9) типа 23, где 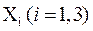 - кодированные значения факторов соответственно, поддерживаемых в каждом конкретном опыте на верхнем
- кодированные значения факторов соответственно, поддерживаемых в каждом конкретном опыте на верхнем = +1, или "+"), либо на нижнем (
= +1, или "+"), либо на нижнем ( = –1, или "–") уровнях, а y u1 и y u2 - отклики объекта в двух сериях параллельных опытов при одних и тех же значениях факторов. Здесь u - номер опыта и соответствующей строки матрицы.
= –1, или "–") уровнях, а y u1 и y u2 - отклики объекта в двух сериях параллельных опытов при одних и тех же значениях факторов. Здесь u - номер опыта и соответствующей строки матрицы.



 c использованием материалов [34], ч.1, с. 865 … 88; [45], c. 62 … 63, и лабораторной работы №10.
c использованием материалов [34], ч.1, с. 865 … 88; [45], c. 62 … 63, и лабораторной работы №10.


