К ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ
Обработку результатов ПФЭ или ДФЭ для построения математической модели согласно общепринятой методике производят по специальному алгоритму, насчитывающему 12 шагов [ 21 ], с.139...144 или [32], с. 56 … 62: 1. Рассчитывают построчные (то есть для каждой строки) средние значения отклика:
2. Вычисляют оценки построчных дисперсий:
3. Находят максимальную D max из восьми дисперсий. 4. Рассчитывают сумму всех (т.е.восьми) построчных дисперсий:
где N = 8 (число строк матрицы плана эксперимента). 5. Определяют экспериментальное значение критерия Кохрена: Gэ = D max / S (4)
6. Из таблицы [ 12 ], с.230, приложение 7 или [23], c.87, приложение 4 выбирают теоретическое (табличное) значение критерия Кохрена Gт при доверительной вероятности b = 0,95 и N = 8. 7. Проверяют соблюдение условия однородности построчных диспер-сий, согласно которому должно быть: Gэ £ Gт (5) Если это условие не соблюдается, в исходные данные вкрались грубые ошибки, в результате чего расчёт необходимо повторить.
где Х4 = Х1Х2; X5 = X1X3; X6 = X2X3; X7 = Х1X2X3, причём каждое из кодированных значений факторов берут с учётом его знака, заданного в соответствующих таблицах. Для расчёта коэффициентов b i используют формулы:
9. Вычисляют оценку общей дисперсии воспроизводимости от- клика: D Y = S / N (9)
10. Находят оценки дисперсии найденных коэффициентов:
D bi = D Y / (П ∙ N) (10)
11. Рассчитывают границы доверительного интервала определе- ния каждого из коэффициентов модели:
где tT - теоретическое (табличное) значение критерия Стьюдента, которое при b= 0,95 и числе степеней свободы f = N ·(П - 1) можно найти в [ 12 ], с.226, приложение 2 или [23], c. 85, приложение 1. По доверительному интервалу проверяют значимость коэффициентов модели. Значимым признается коэффициент, абсолютное значение которого превышает соответствующую границу доверительного интервала. В противном случае коэффициент признаётся статистически незначимым. Обычно незначимыми оказываются достаточно малые коэффициенты, определённые со значительной ошибкой вследствие разброса экспериментальных данных. Незначимые коэффициенты следует обнулить. 12. Проверяют адекватность полученной математической модели. Понятие адекватности объяснено в [ 21 ], с.142. Адекватная модель является точной в пределах принятых статистических критериев. В противном случае она носит приближённый характер. Для проверки используют экспериментальное значение критерия Фишера: Fэ = D ад / D Y, (12)
в выражении которого дисперсия адекватности:
где L - число членов уравнения модели, оставшихся после оценки значимости коэффициентов b i, включая свободный член b 0;
Для суждения об адекватности модели из [ 12 ], с.228, приложение 5 или [23], c. 86, приложение 2 выбирают теоретическое (табличное) значение критерия Фишера Fт при доверительной вероятности 0,95 и числах степеней свободы f 1 = N - L и f 2 = N×( П - 1). Условие адекватности математической модели объекта исследования: Fэ £ Fт (14)
Заметим, что при N = L знаменатель формулы (13) обращается в ноль. При этом проверить адекватность модели описанным способом нельзя. В этом случае студент должен описать другую методику оценки адекватности модели [ 12 ], с.143. Дальнейшие (при необходимости) действия исследователя, направленные на достижение адекватности математической модели объекта, описаны в [ 12 ], с.14З; 151...158. Если пренебречь эффектами взаимодействия факторов, то в безразмерном выражении самым сильным фактором Xi оказывается тот, при котором находится наибольший по абсолютному значению коэффициент b i.. Однако с тем, чтобы довеcти исследование до конца, необходимо сравнить силу и направление воздействия на отклик объекта всех факторов iв натуральном выражении. Для этого можно воспользоваться соотношением:
Xi = (x i - x 0i) / D x i, (15)
в котором x 0i - основной уровень фактора, D x i - интервал варьирования фактора в процессе эксперимента. Отсюда сравнению подлежат эффекты изменений факторов на x i - x 0i = 1, то есть на одну единицу измерения, и критерием сравнительной силы воздействия отдельных факторов, взятых в натуральном выражении, служит формула:
D y i = b i DXi = b i / D x i, (16)
где D y i - изменение отклика объекта, соответствующее изменению рассматриваемого фактора на одну единицу измерения. Выполнение расчётов курсовой работы
|


 (1)
(1) где
где  - порядковый номер параллельного номера, общее число которых составляет П. В настоящем задании П = 2.
- порядковый номер параллельного номера, общее число которых составляет П. В настоящем задании П = 2. ,
,  (2)
(2) (3)
(3) 8. Находят предварительные значения коэффициентов b i (i = 0,7), вхо -дящих в состав искомой модели объекта. Всего здесь может быть определено до восьми коэффициентов включительно соответственно восьми членам модели предварительного вида:
8. Находят предварительные значения коэффициентов b i (i = 0,7), вхо -дящих в состав искомой модели объекта. Всего здесь может быть определено до восьми коэффициентов включительно соответственно восьми членам модели предварительного вида: = b 0 + b 1X1 + b 2X2 + b 3X3 + b 4X4 + b 5X5 + b 6X6 + b 7X7, (6)
= b 0 + b 1X1 + b 2X2 + b 3X3 + b 4X4 + b 5X5 + b 6X6 + b 7X7, (6) (7)
(7) (8)
(8) (11)
(11)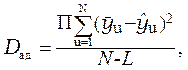 (13)
(13)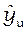 - "модельное" значение отклика в u - й строке матрицы, рассчитанное по уравнению модели.
- "модельное" значение отклика в u - й строке матрицы, рассчитанное по уравнению модели.


