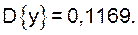Обработка и анализ результатов полного факторного эксперимента с построением математической модели объекта
(2 – й способ) Цель работы, её теоретическое содержание и исходные данные аналогичны представленным в работе №5. Различие проявляется в методике выполнения работы. Для решения задачи используется файл табл. ПФЭ.хls, в которую для экономии учебного времени студентов заранее введено содержание матрицы плана эксперимента (блок данных В3:Н18). Здесь ячейка В3 отображает левый верхний угол – начало блока, а ячейка Н18 – правый нижний угол – конец блока. Символом блока данных является вертикальное двоеточие (:).Данные каждого из двух параллельных опытов последовательно записываются в отдельной строке столбца I таблицы, образуя диапазон данных I 3: I 18 с тем же символом вертикального двоеточия. Каждый из входных (то есть вводимых в компьютер) интервалов значений Y и X удобно выделять перетаскиванием мышью от начала блока (диапазона) до его конца включительно при удерживании в нажатом положении её правой клавиши. После этого они автоматически, практически мгновенно, переносятся в окно “РЕГРЕССИЯ” на места, предварительно помечаемые курсором. Вывод итогов совершаем на отдельный рабочий лист Excel (Лист2), куда сообщаются значения коэффициентов математической модели b 0, b 1, …, b 7, практически совпадающие с полученными при решении задачи №5. Точно так же, коэффициент b 6 следует признать незначимым, так как уровень значимости ошибки его определения В результате доверительная вероятность коэффициента b6 оказывается равной Что касается оценки адекватности полученной математической модели, то Excel формально предлагает пользователю обратить внимание на высокое значение R2 = 0,9966. Это соответствует условию адекватности модели R2 > 0,7 [34], ч.1, с.86…88. Однако, такая оценка в подобных задачах некорректна, поскольку значения факторов Х1, Х2 и Х3 не являются случайными величинами. Поэтому для более строгого заключения об адекватности или неадекватности модели требуется подход, основанный на применении критерия Фишера в соответствии с методикой отечественной математической школы. Вычисленное с помощью Excel значение критерия Фишера F = 339,26 (Лист2) следует игнорировать, а Лист1 нашего файла дополнить следующими расчетами. В столбце J вычислим средние из двух опытов значения отклика Столбец К предназначим для вычисления построчных дисперсий воспроизводимости Du выхода объекта. Столбец L отведём для модельных значений выхода объекта. И, наконец, столбец М пусть содержит построчные значения дисперсий адекватности модели объекта. Все вычисления выполнены по материалам [12], с.142…143 или [23], с. 60…62. В ячейке К18 содержится сумма построчных значений Du, а результат деления её на N = 8 определяет общую дисперсию воспроизводимости выхода Ячейка М18 содержит сумму построчных дисперсий адекватности по столбцу М. Умножив эту сумму на П=2 (число параллельных опытов), получаем значение дисперсии адекватности модели Dад = 0,0541 (ячейка М20) в соответствии с формулой (8.40) [12], с.143, при одном незначимом члене модели здесь N - L=1. Аналогичная формула приведена в [23], с.62 под номером (3.63). Разделив дисперсию адекватности (М20) на дисперсию воспроизводимости выхода (К19), получаем экспериментальное значение критерия Фишера Fэ=0,4629 (ячейка М21). При степенях свободы f 1 = N - L = 1 и f 2 = N(П - 1) = 8 (где N – число опытов без учета дублирования их в параллельных опытах, число которых П=2; N = 23 = 8; L – число членов уравнения математической модели объекта, оставшихся после отсеивания незначащих членов, L = 7) и принятой доверительной вероятности 0,99 табличное значение критерия Фишера FT = 11,3. Заключаем, что Fэ < FT. Отсюда следует, что модель адекватна объекту, то есть соответствует полученным от него экспериментальным данным.
|

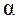 , обозначаемый как Р – значение, слишком велик (0,5245).
, обозначаемый как Р – значение, слишком велик (0,5245). что намного ниже требуемой (
что намного ниже требуемой ( = 0,99).
= 0,99). при одинаковых значениях факторов (формулы, по которым произведены вычисления в блоке ячеек J3:M17, отображаются в строке формул – в верхней части экрана монитора при наведении курсорной рамки на ячейку с результатами вычислений по данной формуле).
при одинаковых значениях факторов (формулы, по которым произведены вычисления в блоке ячеек J3:M17, отображаются в строке формул – в верхней части экрана монитора при наведении курсорной рамки на ячейку с результатами вычислений по данной формуле).