Решение. Для решения используем систему электронных таблиц Excel (Microsoft Office)
Для решения используем систему электронных таблиц Excel (Microsoft Office). На листе 1 блок данных А3:Е37 содержит кодированные значения факторов Х1, Х2, варьируемых на пяти уровнях каждый. Экспериментальные значения отклика объекта занимают интервал F3:F37. Произведем комплексный статистический анализ представленных исходных данных известными командами из главного меню Excel: СЕРВИС | АНАЛИЗ ДАННЫХ | РЕГРЕССИЯ и по запросу компьютера указываем в окне “РЕГРЕССИЯ” интервалы исходных данных аналогично предыдущим работам. На лист 2 выводятся итоги вычислений, из которых нас прежде всего интересуют следующие: 1) критерий R2 = 0,9623 по грубой оценке свидетельствует об адекватности модели; 2) доверительные вероятности a = 1 – “Р – значение” коэффициентов модели (см. данные в интервале Е17:Е22, лист 2) составляют
Отсюда с доверительной вероятностью b = 0,99 значимыми оказываются только первые три коэффициента для линейной модели
что не уcтраивает исследователя. Приняв доверительную вероятность
Аналогичным путем с помощью Excel можно продолжать повышать порядок модели и вычислять её коэффициенты. Напомним, что члены модели с незначимыми коэффициентами (как, например, b 3 в рассматриваемой задаче, где доверительная вероятность b < 0,95) из состава математической модели исключаются. Для строгого суждения об адекватности модели с помощью критерия Фишера необходимо дублирование опытов с последующими дополнительными вычислениями, как это было сделано в предыдущих работах. Поскольку в данном примере параллельные опыты не ставились в силу существенного возрастания общего числа опытов, произведем оценку адекватности с некоторыми упрощениями. Как и выше, дополним “стандартные” вычисления в среде Excel (по столбец F включительно). Найдем модельные значения Чтобы определить дисперсию воспроизводимости выхода с использованием метрологических характеристик применяемой аппаратуры, примем, что измерение
(ячейка Н39). В результате экспериментальное значение критерия Фишера Fэ = Dад / D у = 0,6040. Табличное значение того же критерия по данным [21], с.228 при доверительной вероятности 0,95 составляет FT > 2,09 (ячейка Н41). Таким образом, Fэ < Fт (с большим запасом точности), откуда можно заключить, что полученная математическая модель адекватная. Студенту предлагается произвести дальнейшее усложнение математической модели объекта (что возможно до 4-й степени переменных, проварьированных в рассматриваемом примере на 5 уровнях), и произвести её анализ по той же схеме, которая изложена выше.
|


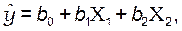
 исследователь получает модель 2 -го порядка в виде
исследователь получает модель 2 -го порядка в виде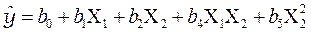 .
.
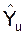 (G3:G37) и дисперсию адекватности модели Dад определением построчных разностей Dад,,u = Yu -
(G3:G37) и дисперсию адекватности модели Dад определением построчных разностей Dад,,u = Yu -  производится на установке класса точности 1,0 с пределами измерения от 10 до 1250 МПа. Тогда [12], с.144
производится на установке класса точности 1,0 с пределами измерения от 10 до 1250 МПа. Тогда [12], с.144



