Определение уравнений состояния по основной передаточной функции
Задача определения уравнений состояния по основной ПФ системы управления в теории дифференциальных уравнений известна как задача приведения линейного уравнения и-го порядка к нормальной форме Коши. Последняя кратко рассмотрена совместно с численными методами при выполнении Лабораторной работы «Построение временных характеристик САУ численным методом». Некоторое отличие задач усматривают в том, что в ТАУ решают неоднородные ОДУ, содержащие не только производные выходной, но и входной величин. Такое уравнение в случае одномерной САУ имеет вид
причем т<п. Операторным представлением рассматриваемого уравнения является ПФ системы
Ф(s)=
Данной ПФ соответствует множество различных уравнений состояния и поставленная выше задача решается неоднозначно. Выбор канонического или иного представления уравнений состояния обусловлен спецификой исследования. Один из возможных вариантов отличается необходимостью принять при моделировании некоторые физические величины в качестве переменных состояния. В этом случае структура матриц Второй из возможных вариантов отличается от первого отсутствием каких-либо требований к физическому содержанию переменных состояния. Выбор канонического представления уравнений состояния осуществляют по другим соображениям. При этом сначала решают проблему минимальной реализации, заключающуюся в поиске такой формы уравнений состояния, которая обеспечивает минимально возможный порядок системы (8). В рассматриваемом случае одномерной САУ с ПФ вида (23) искомые уравнения состояния должны быть /7-го порядка. В общем случае минимальная реализация соответствует невырожденным (полностью управляемым и полностью наблюдаемым) системам. После решения проблемы минимальной реализации выбирают каноническое представление уравнений состояния. Причем выбор канонической формы облегчают известные рекомендации. Например, первое управляемое представление целесообразно использовать при решении задач линейного оптимального управления, а также при решении некоторых задач фильтрации и т.д. /12/. После решения проблемы минимальной реализации уравнений состояния и выбора канонического представления определяют форму ММ. Последняя может иметь вид: - системы дифференциальных уравнений (12), (15)-(19), (21); - матричных уравнений (8); - структурной алгоритмической схемы (рисунки 3-8). Законченный вид ММ приобретает после подстановки в названные уравнения или схему числовых значений коэффициентов. Наиболее просто получают ММ во втором управляемом (УКП) и наблюдаемом представлении. В этом случае элементы матриц соответственно А, С и А, В формируют из коэффициентов числителя и знаменателя ПФ (23). Так, например, если основная ПФ системы уравнения
Ф(s)=
то УКП этой системы (п=3) имеет вид
На рисунке 9 изображена структурная схема САУ соответственно рассматриваемому представлению.
Рисунок 9 - Структурная схема
|


 =
= 
 (22)
(22) (23)
(23) А, В, С и D оказывается заданной и задача сводится к нахождению некоторых их элементов. Эту задачу решают методом неопределенных коэффициентов.
А, В, С и D оказывается заданной и задача сводится к нахождению некоторых их элементов. Эту задачу решают методом неопределенных коэффициентов.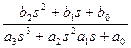 (24)
(24)




