Каноническая форма Жордана
Это представление уравнений состояния также отличается специальным видом матрицы коэффициентов А, которая в данном случае имеет форму Жордана
где корни характеристического уравнения САУ A(s)=0. Как видно, матрица коэффициентов А является диагональной. Это свойство матрицы упрощает вычисления, т.к. матрица Жордана имеет наибольшее количество нулевых элементов. Матрицы входа и выхода в рассматриваемом представлении являются векторами соответственно В = [l 1... l]T и С =[c Следовательно, одномерную САУ описывают уравнениями состояния и выхода вида
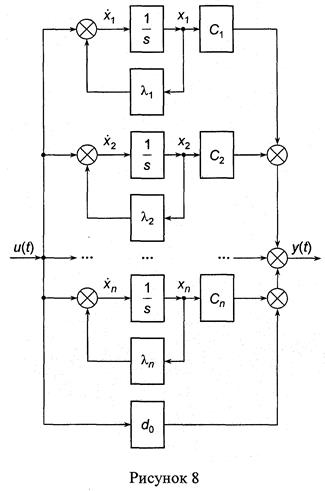
Структурная схема САУ, соответствующая уравнениям (21), изображена на рисунке 8.
Коэффициенты c
где Ф(s) = В общем случае характеристическое уравнение САУ D(s) = 0 имеет п различных действительных корней
D(s)=
а ПФ системы можно разложить на сумму элементарных дробей
Ф(s)= Разложение ПФ на простейшие дроби (компоненты) обусловливает диагональную форму Жордана матрицы А только при отсутствии кратных корней характеристического уравнения. Рассматриваемый метод канонического разложения применяют в случае действительных корней комплексные корни существенно усложняют расчет. Каноническая форма Жордана удобнее тем, что ММ САУ n-го порядка представляет собой систему уравнений п независимых подсистем первого порядка (16), что упрощает расчет динамики САУ.
|
- собственные числа матрицы А, которые рассчитывают как
c 
… сп], a D - скаляром вида D = d 
.
- основная ПФ САУ.
