Описание линеuйных САУ переменными состояния
Линейную САУ описывают системой ОДУ в нормальной форме Коши
или в матричной форме
Таким образом, в компактной векторно-матричной форме САУ может быть описана при помощи уравнения
в котором Для полного описания САУ к уравнениям состояния (1) или (2) добавляют уравнения связи между переменными состояния x(t), x2(t)...,xn(t) и выходными переменными y
(4)
или в векторно-матричной форме
где Таким образом, в общем виде САУ описывают векторно-матричными уравнениями
где Первое из этих уравнений - собственно уравнение состояния, описывает изменение состояния САУ во времени в зависимости от начальных условий (НУ) и входного воздействия U. Второе уравнение - уравнение выхода, устанавливает связь между текущими (мгновенными) значениями переменных состояния X и входных переменных U, с одной стороны, и выходных переменных У - с другой. Другими словами, уравнение состояния описывает динамику САУ, а уравнение выхода является "статическим" соотношением. Второе слагаемое этого уравнения D • U отражает прямую связь (не динамическую) выхода со входом (рисунок 2).
Часто
В этом случае уравнение (5) называют часто уравнением наблюдения. Известно, что не все переменные САУ наблюдаемы (измеримы). Наблюдаемыми являются лишь те, которые составляют вектор выхода У. Среди измеримых переменных обычно находятся и управляемые переменные. Математические модели САУ вида системы уравнений (6) и (7) считают третьей стандартной формой ММ. Как было отмечено, векторно-матричные уравнения (7) описывают многомерную САУ. Эта же совокупность уравнений служит ММ одномерной САУ, т.е. системы с одним входом и одним выходом. При использовании МПС такие САУ часто называют системами со скалярным входом и выходом, т.к. входная и выходная величины являются скалярными. Уравнения состояния и выхода одномерной системы имеют вид
где
Существенным считают структуру матриц. Матрицы подобной структуры относят к матрицам произвольного вида. Одной из задач МПС является преобразование матриц произвольного вида к матрицам специального вида.
|



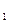 =
= 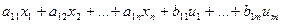 ,
, =
=  , (1)
, (1)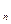
 =
= 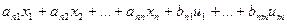 ,
,
 ,(3)
,(3)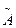 - квадратная матрица [п х п], называемая матрицей коэффициентов, а
- квадратная матрица [п х п], называемая матрицей коэффициентов, а  - прямоугольная матрица [п х т], называемая матрицей управления.
- прямоугольная матрица [п х т], называемая матрицей управления.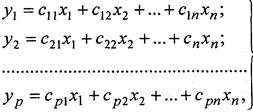
 (5)
(5)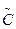 - прямоугольная [р х п] матрица, называемая матрицей выхода.
- прямоугольная [р х п] матрица, называемая матрицей выхода.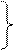
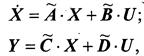
 - прямоугольная [р х п] матрица, называемая матрицей обхода системы.
- прямоугольная [р х п] матрица, называемая матрицей обхода системы.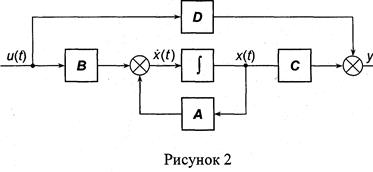
 = 0. Тогда
= 0. Тогда

 (7)
(7)

 ,
,  ,
,  (9)
(9)


