Понятие пространства состояний
1.1 Изучение метода построения математической модели САР типа «вход -состояние - выход».
1.2 Изучение канонических форм уравнений состояния.
1.3 Разработка математической модели САР угловой скорости методом переменных состояния.
1.4 Изучение техники моделирования САР, описанной уравнениями состояния, в системе MATLAB.
1.5 Изучение техники моделирования САР, описанной уравнениями состояния, в SIMULINK.
2 МОДЕЛИ "ВХОД - СОСТОЯНИЕ - ВЫХОД";
Согласно методу пространства состояний (МПС) все переменные величины, характеризующие САУ, разделяют на три группы: 1) входные переменные или входные (управляющие) воздействия ит; 2) выходные переменные у воздействия; 3) переменные (координаты) состояния хп, характеризующие динамическое поведение САУ. Взаимосвязь названных переменных поясняют схемой САУ, на которой систему изображают в виде "черного ящика" (рисунок 1). Отдельные части САУ характеризуют ПФ W схемы, переменные состояния хп являются промежуточными величинами. Их относят к содержимому черного ящика".Следовательно, они скрыты от прямого наблюдения. Кроме того, переменные состояния не всегда являются физическими величинами. Иногда для удобства математического моделирования САУ целенаправленного отказываются от физического содержания переменных состояния. Поэтому в общем случае xn(t) являются абстрактными переменными. Однако, они должны однозначно выражаться через физические величины y В общем случае исследуемую САУ считают многомерной (рисунок 1). Для упрощения работы с многомерными величинами их представляют в векторно-матричном виде. Так, совокупность входных переменных представляют в виде вектора входа
U = совокупность выходных переменных - в виде вектора выхода Y =
асовокупность переменных состояния - в виде вектора состояния X =
Согласно МПС множество всех значений, которые может принять вектор входа U в момент времени t, образует пространство входа исследуемой САУ. Аналогично, множество всех значений, которые может принять вектор выхода Y в момент времени t, образует пространство выхода, а множество всех значений, которые может принять вектор состояния X в момент времени t, образует пространство состояний САУ.
|

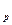 , характеризующие реакцию САУ на входные
, характеризующие реакцию САУ на входные (s) и W
(s) и W  (s). Как следует из
(s). Как следует из
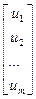 или U=
или U= 
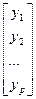 или Y=
или Y= 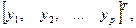
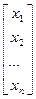 или X=
или X= 



