Управляемое каноническое представление
Второй управляемой канонической формой или управляемым каноническим представлением (УКП) называют специальные матрицы
Матрица коэффициентов А имеет характеристический полином
Очевидно, что коэффициенты характеристического полинома A(s) составляют последнюю строку матрицы коэффициентов А. Коэффициенты характеристического полинома таких матриц определяют без вычислений, т.к. матрица коэффициентов (13) является матрицей Фробениуса. Матрица входа В рассматриваемой канонической формы также имеет специальный вид. Вследствие скалярного входного воздействия матрица В представляет собой вектор-столбец. Его элементы также не требуется вычислять. К матрице С таких специальных требований не предъявляют. В рассматриваемом случае С =[1 О О... 0]. Рассматриваемое УКП отличается также переменными состояния. В качестве последних принимают выходную (управляемую) величину y(t) и (n-1) ее производных
Такие переменные являются нормальными (см. Лабораторную работу «Построение временных характеристик САУ численным методом»). В связи с этим рассматриваемую вторую управляемую каноническую форму или УКП называют нормальной формой. Таким образом, одномерная САУ описывается уравнениями состояния в данной канонической форме (УКП)
Очевидно, что первые п уравнений системы (15) имеют нормальную форму Коши. Полученная ММ системы управления может быть изображена в виде структурной схемы, представленной на рисунке 4.
Рисунок 4
В более общем случае, когда вектор выхода С = [ с схема САУ приобретает каноническую форму с общим выходом, как показано на рисунке 5. Такую САУ описывают уравнениями состояния
Следовательно, в векторно-матричном уравнении состояния матрица коэффициентов имеет форму Фробениуса (13)
|






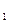 c
c  ... сп], структурная
... сп], структурная





