Лекальні криві – це лінії, які не можуть бути викреслені з допомогою циркуля, і їх побудова виконується по ряду точок. При викреслюванні кривої отриманий ряд точок з’єднується по лекалу, тому її називають лекальною кривою лінією.
Лекальні криві бувають закономірні (форма кривих визначається рівнянням) і незакономірні. Поширеними закономірними лекальними кривими є, наприклад, еліпс, парабола, гіпербола, циклоїда, епіциклоїда, гіпоциклоїда, евольвента, спіраль Архімеда, синусоїда і ін.
Для викреслювання лекальної кривої визначають ряд точок, які з’єднують кривою за допомогою лекал. Кривизну ділянки лекала кожен раз підбирають так, щоб по ньому можна було з’єднати не менше чотирьох точок одночасно. Але з’єднувати слід не всі точки обраної ділянки, а лише перші три точки. Наступна ділянка повинна перекривати раніше обведену і т.д. Точність побудови лекальної кривої підвищується зі збільшенням кількості проміжних точок на ділянці кривої. Лекальні криві використовуються при побудові обрисів багатьох технічних деталей: профілів зубів, кулачків, підшипників і ін.
Дані для побудов лекальних кривих наведені у таблиці 2.3.
Еліпс. Еліпсом називається плоска замкнута крива, яка є геометричним місцем точок, сума відстаней від яких до двох заданих точок F1 та F2, що називаються фокусами, є величина стала.
Парабола. Параболою називається крива лінія, яка є геометричним місцем точок (I, II, III, IV) площини, які є рівновіддаленими від даної точки (що називається фокусом), і даної прямої тієї ж площини (директриси параболи).
Спіраль Архімеда. Спіраллю Архімеда називається плоска крива, що описується точкою, яка рівномірно рухається по радіусу-вектору, який в той же час рівномірно обертається в площині навколо нерухомої точки.
Завдання 2. Виконати графічну частину роботи «Побудова лекальної кривої».
1. За варіантом визначити вид лекальної кривої і її параметри (табл.2.4)
2. За таблицею 2.3 знайти опис побудови даної кривої за заданими параметрами.
3. Виконати в тонких лініях побудову лінії.
4. Нанести розміри, які характеризують параметри кривої.
5. Виконати наведення ліній кресленика.
6. Всі лінії побудов залишити на кресленику.
Таблиця 2.1
Геометричні побудови. Спряження.
| 1.Спряження двох прямих, що перетинаються під прямим кутом, з допомогою дуги заданого радіуса RC.
|   
| Провести дугу АВ радіусом RC із центра кута. Із точок А і В провести допоміжні дуги радіусом RC – визначити центр спряження О. Радіусом RC провести дугу з центром в точці О.
|
| 2.Спряження двох прямих, що перетинаються під гострим кутом, з допомогою дуги заданого радіуса RC.
|   
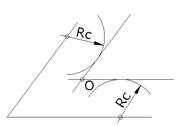
| Провести прямі, паралельні сторонам кута на віддалі R. Визначити центр спряження – точку О. Із точки О опустити перпендикуляри на сторони кута, отримати точки спряження. Радіусом RC провести дугу.
|
| 3.Спряження двох прямих, що перетинаються під тупим кутом, з допомогою дуги заданого радіуса RC.
|   
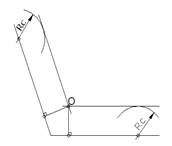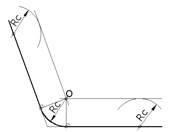
| Провести прямі, паралельні сторонам кута на віддалі R. Визначити центр спряження – точку О. Із точки О опустити перпендикуляри на сторони кута, отримати точки спряження. Радіусом RC провести дугу.
|
Продовження таблиці 2.1
| 4. Зовнішнє спряження дуги кола і прямої з допомогою дуги заданого радіуса RC.
|   
| На відстані RC провести пряму, паралельну заданій прямій, а із центра кола радіусом RC+ R1 – дугу кола. Точка О – центр дуги спряження. Визначити точки спряження: точку 1 - на прямій, точку 2 – на колі. Радіусом RC провести дугу.
|
| 5. Внутрішнє спряження дуги кола і прямої з допомогою дуги заданого радіуса RC.
|    
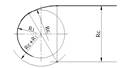
| На відстані RC провести пряму, паралельну заданій прямій, а із центра кола радіусом RC-R1 – дугу кола. Точка О – центр дуги спряження. Визначити точки спряження: точку 1 - на прямій, точку 2 – на колі. Радіусом RC провести дугу.
|
| 6. Зовнішнє спряження дуг двох кіл радіусів R1 і R2 з допомогою дуги заданого радіуса RC.
|    
| Із центрів кіл провести дуги радіусами RС+R1 та RС+R2. Отримаємо точку О – центр дуги спряження. З’єднуємо точку О з центрами кіл – отримаємо точки спряження. Радіусом RC проводимо дугу спряження.
|
Продовження таблиці 2.1
| 7. Внутрішнє спряження дуг двох кіл радіусів R1 і R2 з допомогою дуги заданого радіуса RC.
|    
| Із центрів кіл провести дуги радіусами RС-R1 та RС-R2. Отримаємо точку О – центр дуги спряження. З’єднуємо точку О з центрами кіл – отримаємо точки спряження. Радіусом RC проводимо дугу спряження.
|
| 8. Змішане спряження дуг двох кіл радіусів R1 і R2 з допомогою дуги заданого радіуса RC.
|    
| Із центрів кіл провести дуги радіусами RС-R1 та RС+R2. Отримаємо точку О – центр дуги спряження. З’єднуємо точку О з центрами кіл – отримаємо точки спряження. Радіусом RC проводимо дугу спряження.
|
| |
| | | Варіанти завдань до графічної частини „ Побудова спряження”
| |
Продовження таблиці 2.2
Продовження таблиці 2.2
Продовження таблиці 2.2
Таблиця 2.3
Геометричні побудови. Лекальні криві.
| Парабола
| 
| Розглянемо спосіб побудови параболи за напрямом осі, вершині і одній із точок на її обрисі. Прямі ОЕ і ЕС розділити на однакову кількість рівних частин. Перетин променю
О-3 з прямою паралельною до осі ОО1 і проведеною через точку 3’, яка знаходиться на прямій ОЕ, визначає точку ІІІ, яка належить обрису параболи. Аналогічно знаходять положення точок І, ІІ і т.д.
|
| Спіраль Архімеда
| 
| Розглянемо побудову спіралі Архімеда за заданим центром і кроком. Будуємо коло діаметром D. Коло і радіус кола ділимо на 12 рівних частин. Через точки ділення кола 1’, 2’,…,12’ і центр кола проводимо промені, на яких із центра О відкладаємо відрізки, рівні відповідно 1/12, 2/12, і т.д. кроку спіралі.
Лекальна крива, що з’єднує отримані на променях точки, і буде шуканою спіраллю.
|
| Еліпс
| 
| Відрізок АВ називають великою віссю, а відрізок СД – малою віссю еліпса. Із центра О проводимо два допоміжних концентричних кола, діаметри яких рівні осям еліпса. Ділимо велике коло, наприклад, на 12 частин. Через точку О і точки ділення 1, 2,…,12 проводимо низку прямих. Із точок ділення великого кола проводять прямі паралельні до малої осі еліпса, а із точок ділення малого кола – прямі паралельні до великої осі еліпса. Отримані на перетині точки I, II,…,XII є шуканими точками еліпса. Існують і інші способи побудови еліпса.
|
Таблиця 2.4
Варіанти до завдання «Побудова лекальних кривих»
| Номер варіанту
| Назва кривої
| Дані для побудови, мм
|
|
| Еліпс
| АВ=100, CD=60
|
|
| АВ=90, CD=50
|
|
| АВ=110, CD=80
|
|
| АВ=100, CD=70
|
|
| АВ=110, CD=60
|
|
| АВ=100, CD=50
|
|
| Парабола
| АВ=140, CD=80
|
|
| АВ=120, CD=90
|
|
| АВ=150, CD=70
|
|
| АВ=100, CD=60
|
|
| АВ=110, CD=70
|
|
| АВ=120, CD=50
|
|
| Спіраль Архімеда
| D=120
|
|
| D=100
|
|
| D=80
|
|
| D=140
|
|
| D=160
|
|
| D=90
|
2.3. Поділ кола на рівні частини
Завдання 3. Виконати графічну частину роботи «Поділ кола на рівні частини».
1. За таблицею 2.6 визначити варіант завдання.
2. За таблицею 2.5 вивчити порядок графічного поділу кола на рівну кількість частин.
3. Виконати в тонких лініях побудову деталі.
4. Нанести розміри елементів деталі.
5. Виконати наведення ліній кресленика.
6. Всі лінії побудов залишити на кресленику.
Таблиця 2.5
Поділ кола на рівні частини за допомогою циркуля
| Поділ кола
на 4 і 8 рівних частин
|  
|
| Поділ кола
на 3 і 6 рівних частин
|  
|
| Поділ кола
на 5 рівних частин
|  
|
| Поділ кола
на 7 рівних частин
|  
|
Таблиця 2.6
Варіанти завдань «Поділ кола на рівні частини»
1. Прокладка
| 
2. Кришка
|
3. Прокладка
| 
4. Пластина
|
5. Фланець
| 
6. Пластина
|
Продовження таблиці 2.6
7. Кришка
| 
8. Пластина
|
9. Решітка
| 
10. Фланець
|
11. Кришка
| 
12. Кришка
|
Продовження таблиці 2.6
13. Фланець
| 
14. Фланець
|
15. Пластина
| 
16. Прокладка
|
17. Прокладка
| 
18. Решітка
|
МЕТОДИКА
