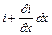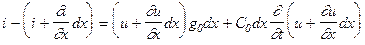ДИФЕРЕНЦІЙНІ РІВНЯННЯ ОДНОРІДНОЇ ЛІНІЇ
Напруга і струм в лінії є функціями двох незалежних перемінних: просторової координати х, що визначає місце спостереження, та часу t, який визначає момент спостереження. Нашою задачею є знаходження просторово-тимчасового розподілу величини струму у лінії i(x, t) та напруги поміж дротами u(х, t). Складемо диференційні рівняння, яким задовольняють напруга і струм у будь-якому перетині двохпровідної лінії. Домовимося називати верхній дріт (рис.3) двохпровідної лінії прямим, а нижній - зворотним. Позитивні напрями струму та напруги оберемо, як показано на рис 3. Хай відомі первинні параметри однорідної лінії: r0 - опір прямого та зворотного дротів, L0 - індуктивність петлі, що утворюється прямим та зворотним дротами, g0 - провідність (відплив) поміж дротами. С0 - ємність між дротами. Довгу лінію можна уявити у вигляді множини сполучених у ланцюжок нескінченно малих елементів довжиною dx, кожний з яких має опір r0dx та індуктивність L0dx, провідність g0dx і ємність C0dx (рис.3). Опір r0dx та індуктивність L0dx будемо рахувати включеними у один дріт. Позначимо через х відстань від початку лінії до поточного елемента її довжини. Миттєві значення напруги та струму на початку обраного елемента лінії dx позначимо через u та i, а на початку наступного - через
Рис. 3
Для елемента лінії довжиною dx на підставі законів Кірхгофа
Наводячи подібні члени і нехтуючи величиною другого порядку малості та скорочуючи на dx, одержуємо диференційні рівняння
(1.1)
Ці рівняння називають телеграфними рівняннями. Вони можуть бути вирішені однозначно при використанні початкових й граничних умов. Початковими умовами будуть значення напруги та струму на початку або в кінці лінії в момент часу, прийнятий за нуль. Граничні умови визначаються зв'язками між напругою та струмом на початку або в кінці лінії, які залежать від заданого режиму роботи лінії. Розв'язання зазначених вище рівнянь дає функціональні залежності напруги та струму у лінії від перемінних х та t.
|


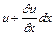 та
та