ПЕРІОДИЧНИЙ РЕЖИМ В ОДНОРІДНІЙ ЛІНІЇ
Розглянемо періодичний режим в довгій лінії при синусоїдальній напрузі джерела живлення. Позначимо комплексні діючі значення напруги та струму на відстані х від початку лінії через Застосовуючи комплексну форму запису, одержуємо на підставі (1.1):
Де Z0 = r0+jL0w - комплексний опір та Y0 = g0+jC0w - комплексна провідність лінії одиничної довжини. Зважаючи на те, що комплексні величини Продифференцюємо рівняння (1.2):
і замінимо
Де Позначимо квадратний корінь з комплексного множника при
Назвемо цю величину коефіцієнтом розповсюдження. Рівняння (1.3) та (1.4) записуються у виді
Маємо однакові однорідні лінійні диференційні рівняння другого порядку. Рішення лінійного диференційного рівняння другого порядку з постійними коефіцієнтами має вигляд
Де Струм
чи
Де
називається хвильовим опором лінії. Хвильовий опір і коефіцієнт розповсюдження називаються вторинними параметрами однорідної лінії. Миттєве значення напруги у точці x рівно явної частини виразу
Тут y1 та y2 - аргументи комплексних величини Миттєве значення струму має вигляд
де Таким чином, миттєві значення напруги і стуму у будь-якій точці лінії складаються з двох функцій. Кожен з додатків можна розглядати як біжучу хвилю, яка рухається в напрямку зростання чи зменшення координати х та згасаючу в напрямку руху. Кожен з додатків в будь-якій фіксованій точці х = x1 подає собою гармонійну функцію з постійною амплітудою. Якщо ж лічити момент часу t фіксованим і розглядати зміну миттєвої напруги вздовж лінії (т. ч. в залежності від х), то отримаємо згасаючу гармонійну хвилю напруги (струму), амплітуда якої Величина a, що характеризує зміну амплітуди хвилі на одиницю довжини лінії, називається коефіцієнтом згасання, а величина b, що характеризує зміну фази на одиницю довжини лінії, називається коефіцієнтом фази. Згасання амплітуди хвилі вздовж лінії обумовлюється втратами в лінії, а зміна фази кінцевою швидкістю розповсюдження електромагнітних коливань. Обидва коефіцієнта a та b входять в комплексний параметр g=a+jb, який характеризує розповсюдження хвилі напруги та струму по лінії. Основними характеристиками біжучої хвилі є фазова швидкість та довжина хвилі. Фазовою швидкістю Аналогічне дослідження другого додатку правої частини рівності (1.10) дало би для фазової швидкості таке ж значення, але із зворотним знаком. Звідси укладаємо, що ці додатки можуть розглядатися як хвилі, які рухаються у протилежних напрямках. Довжиною хвилі l називається відстань між найближчими двома точками, взятих в напрямі розповсюдження хвилі, фази коливання у яких розрізнюються на Хвилю, яка рухається від початку лінії, називають прямою, а яка рухається від кінця лінії - оберненою (зустрічною). Згасаюча пряма хвиля представлена на рис.4. Для її зображення будують обвідні
Рис. 4
Оберемо позитивні напрями напруг та струмів окремих хвиль. Так як обидва додатки в правій частині рівняння (1.7), що визначають напругу U, входять із позитивними знаками, то обираємо позитивними напрямами напруг прямої і оберненої хвиль напрями, які співпадають із позитивним напрямом напруги Для струму існують дві можливості. Можна залишити обидва додатки в правій частині рівності (1.8) із різними знаками або ж поставити між додатками знак плюс, а мінус включити в склад другого додатка. Будемо визначати струм У відповідності із цим можна записати
де Напруга та струм прямої і відповідно оберненої хвиль зв'язані законом Ома:
Це співвідношення пояснює зміст назви Запроваджені поняття про пряму та обернену хвилі у лініях при синусоїдному встановленому режимі полегшують уявлення та аналіз процесів. Фізично існують у лінії тільки результуючі струм Криві розподілу миттєвих значень напруг та струмів також мають хвилеподібний характер (рис.5). Вони показують, що в кожний момент часу результуючі струми та напруги, а також струми та напруги прямої та оберненої хвиль, у різних точках лінії можуть розрізнятися не тільки по значенню, але й по знаку.
Рис. 5
Постійні інтегрування
звідкіля Введемо поняття коефіцієнту відбивання хвилі на початку лінії:
Де Підстановка виразу для
Якщо задані граничні умови на кінці лінії, то краще відраховувати відстань від кінця, прийнявши координату х'. Замінюючи у рівняннях (1.7) та (1.8) х на (l - х)' й використовуючи задані граничні умови
Підставив їх до (1.7) та (1.8), отримаємо остаточні вирази для
Де аналогічно попередньому n2 - коефіцієнт відбивання у кінці лінії:
Система рівнянь (1.14) може бути переписана у наступному виді.
Рівняння (1.14) та (1.16) подають собою рівняння лінії у показовій (або хвильовій) формі при відліку відстані від кінця лінії. Вони перетворюються за допомогою гіперболічних функцій:
Поклавши у цих рівняннях х' = l, отримаємо рівняння лінії у гіперболічній формі, що виражають напругу та струм на початку через напругу та струм у кінці лінії:
Показова і гіперболічна форми запису рівнянні лінії (1.14) та (1.17) взаємно доповнюють друг друга й застосовуються в залежності від умов задачі.
|

 та
та  .
. (1.2)
(1.2)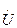 та
та 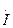 не залежать від t і є лише функціями х, при переході від рівнянь (1.1) до (1.2) часткові похідні по х замінені звичайними.
не залежать від t і є лише функціями х, при переході від рівнянь (1.1) до (1.2) часткові похідні по х замінені звичайними. (1.3)
(1.3) та
та  згідно (1.2). В результаті отримаємо
згідно (1.2). В результаті отримаємо (1.4)
(1.4)
 (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7) - комплексні постійні інтегрування.
- комплексні постійні інтегрування. знаходиться підстановкою (1.7) у перше рівняння (1.2)
знаходиться підстановкою (1.7) у перше рівняння (1.2)
 (1.8)
(1.8) (1.9)
(1.9)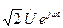 .
. (1.10)
(1.10) та
та  .
.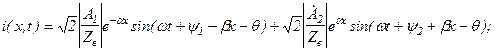 (1.11)
(1.11) .
.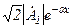 зменшується із зростанням х, т. ч. по мірі відходу від початку лінії до кінця.
зменшується із зростанням х, т. ч. по мірі відходу від початку лінії до кінця. хвилі називається швидкість переміщення фази коливання, що впродовж часу t та по мірі збільшення відстані х, пройденого хвилею, залишається постійної, т. ч.
хвилі називається швидкість переміщення фази коливання, що впродовж часу t та по мірі збільшення відстані х, пройденого хвилею, залишається постійної, т. ч. 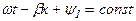 , звідкіля слідує, що
, звідкіля слідує, що  і
і 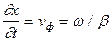
 . Отже, для першого додатку рівності (1.10) отримаємо
. Отже, для першого додатку рівності (1.10) отримаємо  , звідки
, звідки  і
і  , т. ч. за час, рівний періоду, хвиля пробігає відстань, рівну довжині хвилі. Одержана формула виражає залежність, існуючу між довжиною хвилі і коефіцієнтом фази лінії.
, т. ч. за час, рівний періоду, хвиля пробігає відстань, рівну довжині хвилі. Одержана формула виражає залежність, існуючу між довжиною хвилі і коефіцієнтом фази лінії. і вписують хвилю в область, обмежену обвідними.
і вписують хвилю в область, обмежену обвідними.
 , т. ч. від прямого дроту лінії до зворотного.
, т. ч. від прямого дроту лінії до зворотного. ;
; ,
, ;
; 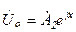 .
. .
. - хвильовий опір.
- хвильовий опір.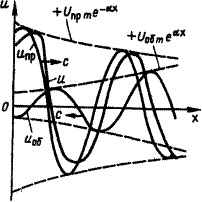
 ;
; ,
, ;
;  .
. , (1.12)
, (1.12)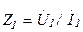 - вхідний опір лінії.
- вхідний опір лінії. (1.13)
(1.13) ;
;  одержуємо для
одержуємо для  ;
;  .
. (1.14)
(1.14) ; (1.15)
; (1.15) - вихідний опір на кінці лінії або у випадку приймача вхідний опір його.
- вихідний опір на кінці лінії або у випадку приймача вхідний опір його. (1.16)
(1.16) (1.17)
(1.17) (1.18)
(1.18)


