ЛІНІЯ БЕЗ СПОТВОРЕНЬ
Сигнали, які передаються по лінії зв'язку, подають собою сукупність множини різних частот: дискретних - у випадку періодичних несинусоїдних сигналів і безперервний спектр - у випадку неперіодичних сигналів. Передачею сигналу без спотворень називається така передача, при якій форма сигналу на початку й кінці лінії однакова. Таке явище має місце в тому випадку, коли коефіцієнт затухання лінії і відповідно фазова швидкість на всіх частотах однакові. Неоднакове затухання на різних частотах створює так звані амплітудні спотворення, а неоднакова швидкість хвиль на різних частотах - фазові спотворення. Для передачі без спотворень вимагається, щоб коефіцієнт затухання a не залежав від частоти, а коефіцієнт фази b був прямо пропорційному частоті; в останньому випадку фазова швидкість Такий стан має місце за умови, що
В цьому випадку коефіцієнт розповсюдження рівний:
З урахуванням (1.29)
Або
Якщо рахувати, що первинні параметри лінії не залежать від частоти, то коефіцієнт затухання в даному випадку буде постійний:
А коефіцієнт фази - прямо пропорційному частоті:
Лінія, параметри якої задовольняють умові (1.29), називається лінією без спотворень, бо будь-які сигнали розповсюджуються по ній з збереженням їхньої форми. Лінія без спотворень є водночас і лінією з мінімальним затуханням, яке тільки і можливе при заданих параметрах r0 та g0. Хвильовий опір лінії без спотворень - дійсне число, що тотожно активному опору, який не залежить від частоти. У відповідності з (1.22) воно виражається простою формулою
Фазова швидкість в лінії без спотворень постійна і співпадає з виразом для граничної швидкості розповсюдження хвилі вздовж лінії при нескінченно високій частоті:
Для усунення спотворень, що викликаються неузгодженістю опору приймача з опором лінії, т. ч. для запобігання виникненню відбиття на прийомному кінці, опір приймача повинен бути рівний Коефіцієнт корисної дії лінії має в цьому випадку найбільше можливе значення, рівне е-2la, як у лінії при погодженому навантаженні. Зважаючи на те, що хвильовий опір лінії без спотворень є активним, при погодженому навантаженні напруга та струм в будь-якій точці лінії співпадають по фазі. Відношення миттєвих значень напруги та струму в будь-якій точці такої лінії дорівнює:
звідкіля
Отже, на будь-якому відтинку лінії без спотворень, навантаженої погоджено, енергія магнітного поля в кожний момент часу дорівнює енергії електричного поля. Слідує помітити, що на практиці умова (1.29), як правило, не виконується; відношення L0/r0 звичайно значно менш C0/g0. Внаслідок цього затухання лінії завжди перевищує мінімальне. Найменше відповідають умові (1.29) кабельні лінії. Щоб лінія більш відповідала умові (1.29), слід змінити будь-який первинний параметр, наприклад зменшити r0 чи С0 або збільшити g0 чи L0. Зменшення активного опору r0 можливо за рахунок вжиття дротів більшого діаметру, що значно дорожчало би лінію. Збільшення провідності ізоляції g0 невигідно, бо при цьому зросло би затухання лінії. Найкращим засобом для наближення первинних електричних параметрів до оптимального співвідношення (1.29) є штучне збільшення індуктивності увімкненням в лінію через певну відстань індуктивних котушок чи застосування кабелю, жили якого обмотані тонкою стрічкою з матеріалу із високої магнітної проникливості.
|

 є незалежною від частоти.
є незалежною від частоти. (1.29)
(1.29)


 (1.30)
(1.30) (1.31)
(1.31) (1.32)
(1.32)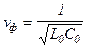
 .
.
 (1.33)
(1.33)


