Вспомогательные неравенства
Предложение 1. Пусть
тогда для любых неотрицательных чисел
Доказательство. Можно полагать, что
Полагая в неравенстве (4.3)
Умножим это неравенство на
Наконец, учитывая соотношение
Предложение доказано. Неравенство Гельдера. Для произвольных чисел
Запишем неравенство (4.2)
и просуммируем по
Используя соотношения
Отсюда следует неравенство Гельдера
Неравенство доказано. Неравенство Гельдера для бесконечных сумм. Пусть даны бесконечные последовательности чисел Предположим, что сходятся числовые ряды
Неравенство Коши-Буняковского получается как частный случай неравенства Гельдера, когда
Доказательство. Полагаем, что существуют интегралы, входящие в правую часть (4.13). Введем следующие обозначения
Применяя неравенство (4.2) к функциям
Проинтегрируем это неравенство и учтем обозначения (4.14). В итоге найдем
Отсюда следует
Неравенство доказано. Интегральное неравенство Коши-Буняковского получается как частный случай, когда
Неравенство Минковского. Для
Доказательство. Достаточно ограничиться случаем Имеем
При
получим
С учетом равенства Неравенство Минковского для бесконечных сумм. Пусть даны бесконечные последовательности чисел Предположим, что сходятся числовые ряды
Интегральное Неравенство Минковского.. Справедливо неравенство
где Доказательство. Имеем
Введем число
Умножая обе части (4.22) на
и учитывая равенство
Так как
4.2. Приложение 2.
|

 и
и  - вещественные числа, связанные соотношением
- вещественные числа, связанные соотношением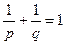 , (4.1)
, (4.1) и
и  имеет место неравенство
имеет место неравенство . (4.2)
. (4.2) . Рассмотрим функцию
. Рассмотрим функцию  , где
, где  , a
, a  , и согласно (4.1)
, и согласно (4.1)  . Найдем производную
. Найдем производную  . Анализ производной показывает, что наибольшего значения функция достигает при
. Анализ производной показывает, что наибольшего значения функция достигает при 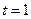 . Поэтому
. Поэтому  или
или . (4.3)
. (4.3) и учитывая связь
и учитывая связь  . (4.4)
. (4.4)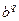
 . (4.5)
. (4.5) , найдем
, найдем .
. и
и  справедливо неравенство Гельдера
справедливо неравенство Гельдера . (4.6) Доказательство. Введем обозначения
. (4.6) Доказательство. Введем обозначения
 ,
, 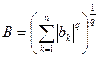 ,
,  ,
,  . (4.7)
. (4.7)
 . В результате получим
. В результате получим . (4.8)
. (4.8) ,
,  и переходя от величин
и переходя от величин  ,
,  к величинам
к величинам  ,
, 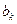 , из (4.8) найдем
, из (4.8) найдем . (4.9)
. (4.9)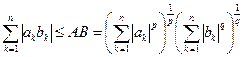 . (4.10)
. (4.10) и
и  .
. ,
,  . Переходя в неравенстве (4.10) к пределу, когда
. Переходя в неравенстве (4.10) к пределу, когда 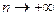 , получим
, получим . (4.11)
. (4.11)
 . (4.12) Интегральное неравенство Гельдера. Имеет место неравенство
. (4.12) Интегральное неравенство Гельдера. Имеет место неравенство . (4.13)
. (4.13)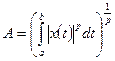 ,
,  ,
,  ,
,  . (4.14)
. (4.14) и
и  , получим
, получим .
.
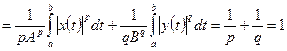 .
. .
.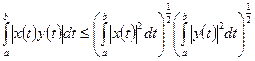 . (4.15)
. (4.15) , произвольных чисел
, произвольных чисел  . (4.16)
. (4.16) ,
,  ,
,  .
. . (4.17)
. (4.17) справедливость неравенства (4.16) очевидна. Полагая
справедливость неравенства (4.16) очевидна. Полагая  , введем
, введем  с тем, чтобы
с тем, чтобы  . (4.18) Заметим, что
. (4.18) Заметим, что  . Умножая обе части (4.18) на
. Умножая обе части (4.18) на ,
, .
.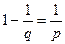 получаем окончательное доказательство неравенства Минковского.
получаем окончательное доказательство неравенства Минковского.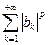 . Переходя в неравенстве (4.16) к пределу, когда
. Переходя в неравенстве (4.16) к пределу, когда  . (4.19)
. (4.19) , (4.20)
, (4.20) и
и 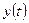 - произвольные функции.
- произвольные функции.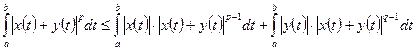 . (4.21)
. (4.21)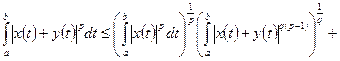
 . (4.22)
. (4.22)
 .
.


