Это равносильно тому, что множество  ограничено в метрическом пространстве
ограничено в метрическом пространстве  .
.
Определение 13. Множество  в метрическом пространстве
в метрическом пространстве  называется равностепенно непрерывным, если для любого
называется равностепенно непрерывным, если для любого  существует такое
существует такое  такое, что для любых
такое, что для любых  ,для которых
,для которых 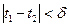 и любой функции
и любой функции 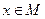 выполнено
выполнено
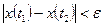 .
.
Теорема 3 (Арцела-Асколи). Для того, чтобы множество 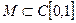 было относительно компактным необходимо и достаточно, чтобы оно было равномерно ограничено и равностепенно непрерывно.
было относительно компактным необходимо и достаточно, чтобы оно было равномерно ограничено и равностепенно непрерывно.
Доказательство. Необходимость. Пусть множество 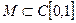 относительно компактно, тогда оно ограничено в пространстве
относительно компактно, тогда оно ограничено в пространстве  , т.е. равномерно ограничено. Нужно проверить равностепенную непрерывность. Зададим
, т.е. равномерно ограничено. Нужно проверить равностепенную непрерывность. Зададим  и построим конечную
и построим конечную 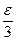 - сеть
- сеть 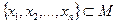 . Функции
. Функции 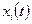 ,
, 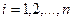 равномерно непрерывны на отрезке
равномерно непрерывны на отрезке 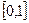 . Поэтому для каждой функции
. Поэтому для каждой функции 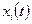 найдется
найдется 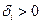 так, чтобы при
так, чтобы при 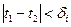 для любых
для любых  выполнялось неравенство
выполнялось неравенство
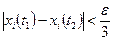 ,
, 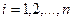 .
.
Положим 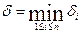 . Тогда для любых
. Тогда для любых  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , и всех
, и всех 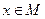 будем иметь неравенство
будем иметь неравенство
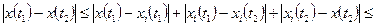
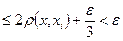 .
.
При выводе последнего неравенства мы учли то, что 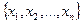 является
является 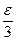 - сеть для множества
- сеть для множества  . Следовательно, доказали равностепенную непрерывность.
. Следовательно, доказали равностепенную непрерывность.
Достаточность. Дано ограниченное и равностепенно непрерывное семейство 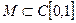 . Необходимо доказать вполне ограниченность
. Необходимо доказать вполне ограниченность  . Из ограниченности следует неравенство
. Из ограниченности следует неравенство
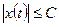 ,
, 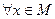 ,
,  .
.
Зададим  и, используя равностепенную непрерывность, найдем
и, используя равностепенную непрерывность, найдем  так, чтобы
так, чтобы
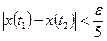
при 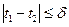 для всех
для всех 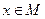 . Затем построим сетку: разобьем отрезок
. Затем построим сетку: разобьем отрезок 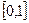 точками
точками  на интервалы длины меньше
на интервалы длины меньше  , а отрезок
, а отрезок  - точками
- точками 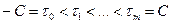 на интервалы длины меньше
на интервалы длины меньше  . Пусть
. Пусть  - семейство непрерывных функций, принимающих в точках
- семейство непрерывных функций, принимающих в точках 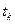 значения
значения 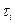 и линейных на отрезках
и линейных на отрезках 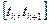 . Это семейство конечно.
. Это семейство конечно.
Докажем, что семейство  является
является 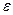 - сетью для множества
- сетью для множества  . По функции
. По функции 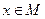 выберем функцию
выберем функцию 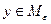 так, чтобы выполнялось неравенство
так, чтобы выполнялось неравенство
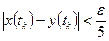 .
.  .
.
Отсюда получим
 .
.
Так как на отрезке 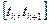 функция
функция  линейна, то
линейна, то
 ,
, 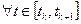 .
.
Наконец, возьмем произвольную точку  из отрезка
из отрезка 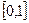 . Тогда найдется
. Тогда найдется  такое, что
такое, что 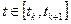 . Отсюда
. Отсюда
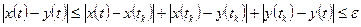 .
.
Из полученного неравенства следует, что семейство  является
является 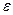 - сетью для множества
- сетью для множества  . Теорема доказана.
. Теорема доказана.
3.4. Относительная компактность в пространствах 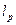 и
и 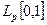
Теорема 4. Множество  в метрическом пространстве
в метрическом пространстве 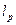 ,
,  , относительно компактно тогда и только тогда, когда выполнены условия:
, относительно компактно тогда и только тогда, когда выполнены условия:
1) существует такое число 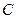 , что
, что 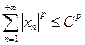 для любых
для любых 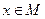 ;
;
2) для любого  существует номер
существует номер 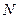 такой, что для всех
такой, что для всех 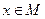 выполнено неравенство
выполнено неравенство 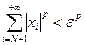 .
.
Необходимость. Условие 1) означает ограниченность множества  в метрическом
в метрическом
пространстве 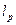 . Оно следует из относительной компактности. Докажем необходимость второго условия. Обозначим
. Оно следует из относительной компактности. Докажем необходимость второго условия. Обозначим
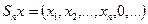 ,
, 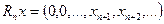 .
.
Тогда 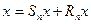 и имеет место соотношение
и имеет место соотношение
 .
.
Очевидно, что 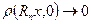 , при
, при 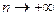 . Далее, справедливо неравенство
. Далее, справедливо неравенство
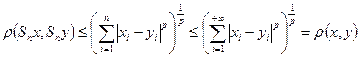 ,
, 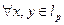 .
.
Возьмем  и построим
и построим 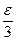 - сеть для множества
- сеть для множества  :
: 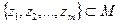 . Тогда для любого
. Тогда для любого 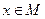 найдется
найдется 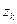 такая, что
такая, что  . Применяя неравенство треугольника, найдем
. Применяя неравенство треугольника, найдем
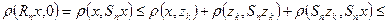
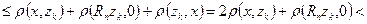
 .
.
Поскольку 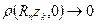 при
при 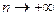 , то найдется число
, то найдется число 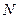 такое, что
такое, что 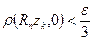 при
при  и всех
и всех  . Тогда
. Тогда 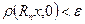 для всех
для всех 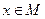 .
.
Достаточность. Для произвольного  выберем
выберем 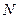 так, чтобы
так, чтобы
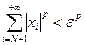 ,
, 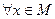
и зафиксируем 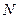 . Каждому
. Каждому 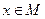 поставим в соответствие
поставим в соответствие 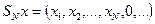 . Очевидно, что
. Очевидно, что 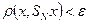 . Кроме того, можно показать, что множество
. Кроме того, можно показать, что множество  является компактным. Следовательно, построена компактная
является компактным. Следовательно, построена компактная 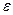 - сеть для
- сеть для  и по следствию к теореме Хаусдорфа, множество
и по следствию к теореме Хаусдорфа, множество  относительно компактно. Теорема доказана.
относительно компактно. Теорема доказана.
Второй способ доказательства достаточности. Выше мы построили компактную 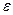 - сеть для
- сеть для  , а теперь построим конечную
, а теперь построим конечную 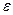 - сеть для
- сеть для  . Выберем
. Выберем 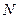 так, чтобы
так, чтобы
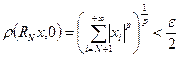 ,
, 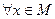 .
.
Возьмем 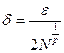 ,
,  и рассмотрим конечное множество
и рассмотрим конечное множество  :
:
 .
.
Докажем, что множество  образует
образует 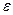 - сеть для
- сеть для  . Для
. Для 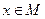 выберем
выберем 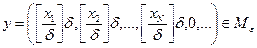 , где
, где  - целая часть числа
- целая часть числа  . Тогда
. Тогда
 .
.
По теореме Хаусдорфа множество  относительно компактно. Теорема доказана.
относительно компактно. Теорема доказана.
В заключение приведем без доказательства критерий относительной компактности в пространстве 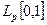 .
.
Теорема 5 (М.Рисс). Множество 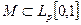 ,
, 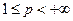 , является относительно компактным тогда и только тогда, когда выполнены условия:
, является относительно компактным тогда и только тогда, когда выполнены условия:
1) существует постоянная 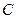 такая, что
такая, что
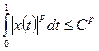 ,
, 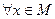 ;
;
2) для любого  существует
существует  такое, что при
такое, что при 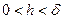
 ,
, 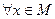 .
.
Доказательство. Пусть  - относительно компактное множество в
- относительно компактное множество в 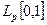 . Относительно компактное множество ограничено, поэтому 1) выполнено. Возьмем
. Относительно компактное множество ограничено, поэтому 1) выполнено. Возьмем  и построим конечную
и построим конечную 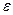 -сеть
-сеть 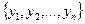 для множества
для множества  . Поскольку каждая функция из
. Поскольку каждая функция из 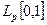 непрерывна в среднем [4], то существует такое
непрерывна в среднем [4], то существует такое  , что при
, что при  верно неравенство
верно неравенство  ,
, 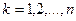 . Возьмем произвольную функцию
. Возьмем произвольную функцию  и найдем такую функцию
и найдем такую функцию 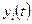 из
из 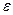 - сети, чтобы
- сети, чтобы  . Тогда, если
. Тогда, если  , то из неравенства треугольника получим
, то из неравенства треугольника получим
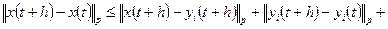
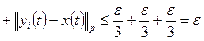 .
.
При этом выводе мы воспользовались тем, что функции 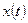 и
и 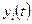 равны нулю вне отрезка
равны нулю вне отрезка 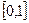 . Тем самым проверено второе условие и необходимость доказана.
. Тем самым проверено второе условие и необходимость доказана.
Достаточность. Вначале выведем вспомогательные неравенства для функций Стеклова 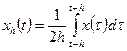 . Имеем
. Имеем
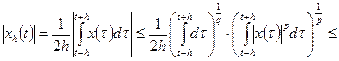
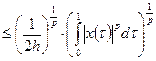 ,
,
и
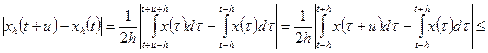
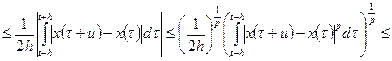
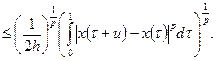
Из условий теоремы 1) и 2) и этих неравенств следует, что при фиксированном 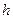 функции семейства
функции семейства 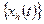 , когда
, когда  равномерно ограничены и равностепенно непрерывны:
равномерно ограничены и равностепенно непрерывны: 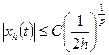 и при
и при 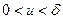
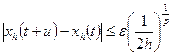 . По теореме Арцела – Асколи любая последовательность этого семейства имеет равномерно сходящуюся подпоследовательность. Эта подпоследовательность также сходится в
. По теореме Арцела – Асколи любая последовательность этого семейства имеет равномерно сходящуюся подпоследовательность. Эта подпоследовательность также сходится в 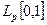 , т. е. семейство
, т. е. семейство 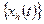 относительно компактно в
относительно компактно в 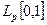 .
.
С другой стороны
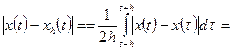
 .
.
Отсюда
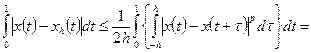
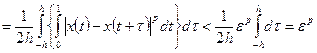 .
.
При этом мы воспользовались вторым условием теоремы, поскольку  .
.
Таким образом, относительно компактное семейство 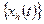 образует
образует 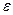 -сеть для множества
-сеть для множества  и по следствию к теореме Хаусдорфа относительно компактно и само множество
и по следствию к теореме Хаусдорфа относительно компактно и само множество  . Теорема доказана.
. Теорема доказана.

 ограничено в метрическом пространстве
ограничено в метрическом пространстве  .
. существует такое
существует такое  такое, что для любых
такое, что для любых  ,для которых
,для которых 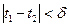 и любой функции
и любой функции 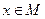 выполнено
выполнено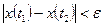 .
.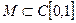 было относительно компактным необходимо и достаточно, чтобы оно было равномерно ограничено и равностепенно непрерывно.
было относительно компактным необходимо и достаточно, чтобы оно было равномерно ограничено и равностепенно непрерывно.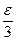 - сеть
- сеть 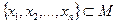 . Функции
. Функции 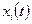 ,
, 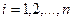 равномерно непрерывны на отрезке
равномерно непрерывны на отрезке 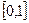 . Поэтому для каждой функции
. Поэтому для каждой функции 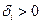 так, чтобы при
так, чтобы при 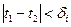 для любых
для любых 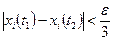 ,
, 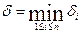 . Тогда для любых
. Тогда для любых  , и всех
, и всех 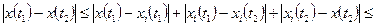
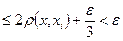 .
.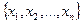 является
является 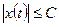 ,
, 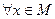 ,
,  .
.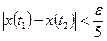
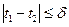 для всех
для всех  на интервалы длины меньше
на интервалы длины меньше  , а отрезок
, а отрезок  - точками
- точками 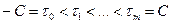 на интервалы длины меньше
на интервалы длины меньше  . Пусть
. Пусть  - семейство непрерывных функций, принимающих в точках
- семейство непрерывных функций, принимающих в точках 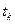 значения
значения 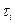 и линейных на отрезках
и линейных на отрезках 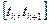 . Это семейство конечно.
. Это семейство конечно.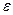 - сетью для множества
- сетью для множества 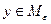 так, чтобы выполнялось неравенство
так, чтобы выполнялось неравенство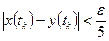 .
.  .
. .
. линейна, то
линейна, то ,
, 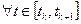 .
. из отрезка
из отрезка  такое, что
такое, что 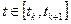 . Отсюда
. Отсюда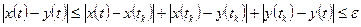 .
.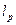 и
и 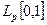
 , относительно компактно тогда и только тогда, когда выполнены условия:
, относительно компактно тогда и только тогда, когда выполнены условия: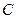 , что
, что 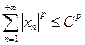 для любых
для любых 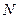 такой, что для всех
такой, что для всех 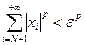 .
.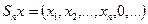 ,
, 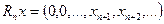 .
.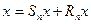 и имеет место соотношение
и имеет место соотношение .
.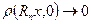 , при
, при 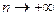 . Далее, справедливо неравенство
. Далее, справедливо неравенство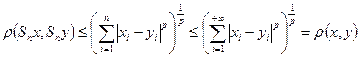 ,
, 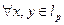 .
.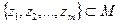 . Тогда для любого
. Тогда для любого 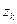 такая, что
такая, что  . Применяя неравенство треугольника, найдем
. Применяя неравенство треугольника, найдем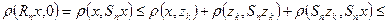
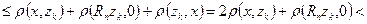
 .
.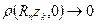 при
при 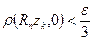 при
при  и всех
и всех  . Тогда
. Тогда 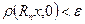 для всех
для всех 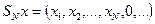 . Очевидно, что
. Очевидно, что 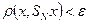 . Кроме того, можно показать, что множество
. Кроме того, можно показать, что множество  является компактным. Следовательно, построена компактная
является компактным. Следовательно, построена компактная 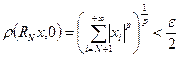 ,
, 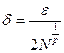 ,
,  и рассмотрим конечное множество
и рассмотрим конечное множество  :
: .
.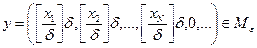 , где
, где  - целая часть числа
- целая часть числа  . Тогда
. Тогда .
.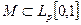 ,
, 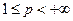 , является относительно компактным тогда и только тогда, когда выполнены условия:
, является относительно компактным тогда и только тогда, когда выполнены условия: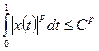 ,
, 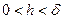
 ,
, 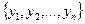 для множества
для множества  верно неравенство
верно неравенство  ,
, 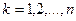 . Возьмем произвольную функцию
. Возьмем произвольную функцию  и найдем такую функцию
и найдем такую функцию 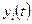 из
из  . Тогда, если
. Тогда, если 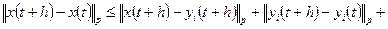
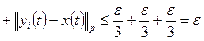 .
.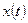 и
и 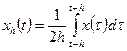 . Имеем
. Имеем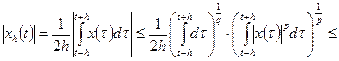
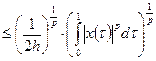 ,
,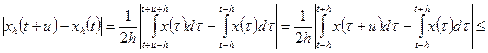
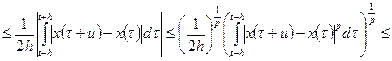
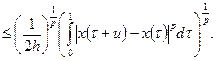
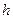 функции семейства
функции семейства 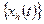 , когда
, когда  равномерно ограничены и равностепенно непрерывны:
равномерно ограничены и равностепенно непрерывны: 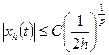 и при
и при 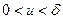
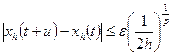 . По теореме Арцела – Асколи любая последовательность этого семейства имеет равномерно сходящуюся подпоследовательность. Эта подпоследовательность также сходится в
. По теореме Арцела – Асколи любая последовательность этого семейства имеет равномерно сходящуюся подпоследовательность. Эта подпоследовательность также сходится в 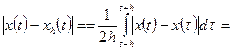
 .
.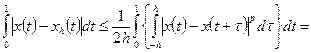
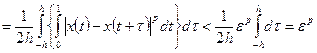 .
. .
.


