Предложение 6. Образ компактного множества при непрерывном отображении компактен.
Доказательство. Пусть  - непрерывное отображение и
- непрерывное отображение и  - компактное множество в
- компактное множество в  . Возьмем произвольную последовательность
. Возьмем произвольную последовательность 
 . Тогда существует последовательность
. Тогда существует последовательность 
 такая, что
такая, что 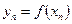 ,
, 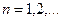 .
.
Последовательности  имеет сходящуюся подпоследовательность:
имеет сходящуюся подпоследовательность:  , причем
, причем 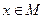 . Тогда в силу непрерывности
. Тогда в силу непрерывности  . Предложение доказано.
. Предложение доказано.
Предложение 7. Образ компактного множества при непрерывном отображении ограничен и замкнут.
Доказательство следует из предложения 6 и того, что компактное множество в метрическом пространстве ограничено и замкнуто. Предложение доказано.
Предложение 8. Пусть  отображает компактное метрическое пространство
отображает компактное метрическое пространство  на числовую прямую
на числовую прямую  . Тогда отображение
. Тогда отображение  ограничено и достигает своей точной верхней и точной нижней грани.
ограничено и достигает своей точной верхней и точной нижней грани.
Доказательство. Числовое множество  , согласно предложения 6, ограничено и замкнуто. А из замкнутости
, согласно предложения 6, ограничено и замкнуто. А из замкнутости  следует, что точная верхняя и точная нижняя грани принадлежат множеству значений. Предложение доказано.
следует, что точная верхняя и точная нижняя грани принадлежат множеству значений. Предложение доказано.
Предложение 9. Любое непрерывное отображение  компактного метрического пространства
компактного метрического пространства  в метрическое пространство
в метрическое пространство  является равномерно непрерывным.
является равномерно непрерывным.
Доказательство. Предположим, что  не является равномерно непрерывным, т.е. не выполняется (1.15). Построим в символической форме отрицание:
не является равномерно непрерывным, т.е. не выполняется (1.15). Построим в символической форме отрицание:
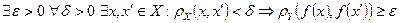 .
.
Используя это отрицание, для каждого 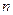 выберем такие
выберем такие 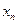 и
и  , что
, что
 ,
,  . (3.4)
. (3.4)
Из последовательности  выберем сходящуюся подпоследовательность
выберем сходящуюся подпоследовательность  .
.
Тогда  , т.е.
, т.е.  .
.
Но отображение  непрерывно, поэтому
непрерывно, поэтому 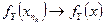 ,
,  и, следовательно,
и, следовательно,  , что противоречит неравенству (3.4). Полученное противоречие и доказывает предложение.
, что противоречит неравенству (3.4). Полученное противоречие и доказывает предложение.
4. ПРИЛОЖЕНИЯ

 - непрерывное отображение и
- непрерывное отображение и  - компактное множество в
- компактное множество в  . Возьмем произвольную последовательность
. Возьмем произвольную последовательность 
 . Тогда существует последовательность
. Тогда существует последовательность  такая, что
такая, что 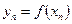 ,
, 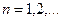 .
. имеет сходящуюся подпоследовательность:
имеет сходящуюся подпоследовательность:  , причем
, причем 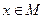 . Тогда в силу непрерывности
. Тогда в силу непрерывности  . Предложение доказано.
. Предложение доказано. отображает компактное метрическое пространство
отображает компактное метрическое пространство  . Тогда отображение
. Тогда отображение  , согласно предложения 6, ограничено и замкнуто. А из замкнутости
, согласно предложения 6, ограничено и замкнуто. А из замкнутости  является равномерно непрерывным.
является равномерно непрерывным.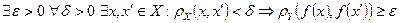 .
.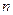 выберем такие
выберем такие 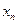 и
и  , что
, что ,
,  . (3.4)
. (3.4) выберем сходящуюся подпоследовательность
выберем сходящуюся подпоследовательность  , т.е.
, т.е.  .
.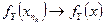 ,
,  и, следовательно,
и, следовательно,  , что противоречит неравенству (3.4). Полученное противоречие и доказывает предложение.
, что противоречит неравенству (3.4). Полученное противоречие и доказывает предложение.


