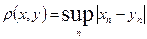Предложение 2. При всех  справедливо соотношение
справедливо соотношение
 . (4.23)
. (4.23)
Это соотношение непосредственно получается из бинома Ньютона.
Предложение 3. При всех вещественных  имеет место неравенство
имеет место неравенство
 . (4.24) Доказательство. Продифференцируем по
. (4.24) Доказательство. Продифференцируем по  тождество
тождество
 (4.25)
(4.25)
и результат умножим на  :
:
 . (4.26)
. (4.26)
Дифференцируя (4.26) и умножая на  , получим
, получим
 . (4.27) Положим в (4.25), (4.26) и (4.27)
. (4.27) Положим в (4.25), (4.26) и (4.27)  и умножим полученные тождества на
и умножим полученные тождества на
 . В результате придем к соотношениям
. В результате придем к соотношениям
 , (4.28)
, (4.28)
 , (4.29)
, (4.29)
 . (4.30)
. (4.30)
Наконец, умножим (4.28) на  , (4.29) на
, (4.29) на  и (4.30) на 1 и все сложим:
и (4.30) на 1 и все сложим:
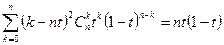 .
.
Отсюда непосредственно получается доказательство утверждения.
Определение 1. Для функции  , заданной на промежутке
, заданной на промежутке  многочлен
многочлен
 (4.31)
(4.31)
называется многочленом Бернштейна.
Теорема 1 (Бернштейн). Если  , то последовательность
, то последовательность  сходится к функции
сходится к функции  в пространстве
в пространстве  , т.е. равномерно на отрезке
, т.е. равномерно на отрезке  .
.
Доказательство. Пусть  . Вследствие равномерной непрерывности на отрезке для любого
. Вследствие равномерной непрерывности на отрезке для любого  найдется такой
найдется такой  , что если
, что если  , то
, то  .
.
Далее из (4.23) следует, что
 .
.
Вычитая из этого равенства (4.30), получим
 . (4.32) Разобьем все числа
. (4.32) Разобьем все числа  на два множества
на два множества  и
и  :
:
 ,
,  .
.
Если  , то
, то  , и на основании утверждения 1 имеем
, и на основании утверждения 1 имеем
 . (4.33)
. (4.33)
Если же  , то
, то  и, используя утверждение 2, получим
и, используя утверждение 2, получим
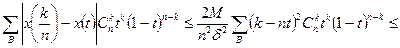
 . (4.34)
. (4.34)
Суммируя (4.33) и (4.34), а также учитывая (4.32), найдем
 ,
,  .
.
Отсюда при  имеем
имеем  ,
,  Теорема доказана.
Теорема доказана.
Теорема 2 (Вейерштрасса). Пусть  . Для любого
. Для любого  существует такой многочлен
существует такой многочлен  , что при всех
, что при всех 
 .
.
Доказательство. Рассмотрим функцию  . Она определена и непрерывна на отрезке
. Она определена и непрерывна на отрезке  . По теореме Бернштейна найдется такой многочлен
. По теореме Бернштейна найдется такой многочлен  , что при всех
, что при всех 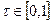
 .
.
Если  , то
, то  и, следовательно, справедливо неравенство
и, следовательно, справедливо неравенство
 .
.
Поэтому многочлен  и является требуемым. Теорема доказана.
и является требуемым. Теорема доказана.
4.3. Приложение 3
Структура открытых множеств на прямой.
Канторово множество.
Здесь мы рассматриваем множества на прямой с обычной евклидовой метрикой.
Предложение 3. В ограниченном сверху замкнутом множестве  есть самая правая точка.
есть самая правая точка.
Доказательство. Положим  . Докажем, что всегда
. Докажем, что всегда  . По определению точней верхней грани для любого
. По определению точней верхней грани для любого  найдется точка
найдется точка  такая, что
такая, что  . Отсюда следует, что точка
. Отсюда следует, что точка  является точкой прикосновения для множества
является точкой прикосновения для множества  и поскольку множество
и поскольку множество  замкнуто, то оно содержит свои точки прикосновения. Также по определению верхней грани точка
замкнуто, то оно содержит свои точки прикосновения. Также по определению верхней грани точка  является правой точкой множества
является правой точкой множества  . Предложение доказано.
. Предложение доказано.
Аналогично всякое ограниченное снизу и замкнутое множество имеет левую точку.
Определение 1. Пусть  - открытое множество. Если интервал
- открытое множество. Если интервал 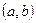 содержится во множестве
содержится во множестве  , а его концы не принадлежат множеству
, а его концы не принадлежат множеству  , то этот интервал называется составляющим интервалом множества
, то этот интервал называется составляющим интервалом множества  .
.
Предложение 4. Если  - непустое ограниченное открытое множество, то каждая его точка принадлежит некоторому составляющему интервалу.
- непустое ограниченное открытое множество, то каждая его точка принадлежит некоторому составляющему интервалу.
Доказательство. Для каждой точки  построим составляющий интервал. Положим
построим составляющий интервал. Положим  . Это множество замкнуто и ограничено снизу, а потому имеет левую точку, которую обозначим через
. Это множество замкнуто и ограничено снизу, а потому имеет левую точку, которую обозначим через  . Очевидно,
. Очевидно,  . Но
. Но  и, поэтому,
и, поэтому,  . Отсюда следует, что
. Отсюда следует, что  .
.
Докажем, что  и
и  . Последнее утверждение следует из того, что
. Последнее утверждение следует из того, что  . Далее, если
. Далее, если  и
и  , то
, то  , а это противоречит тому, что точка
, а это противоречит тому, что точка  - левая точка множества
- левая точка множества  .
.
Аналогично доказывается существование такой точки  , что
, что  и
и  .
.
В результате получаем, что  есть составляющим интервалом множества
есть составляющим интервалом множества  , содержащий точку
, содержащий точку  . Предложение доказано.
. Предложение доказано.
Предложение 5. Любые два составляющих интервала множества  или тождественны или не пересекаются.
или тождественны или не пересекаются.
Доказательство. Пусть два составляющих интервала  и
и  имеют общую точку
имеют общую точку  :
:  ,
,  . Предположим, что
. Предположим, что  . Тогда, очевидно,
. Тогда, очевидно,  , но это невозможно, поскольку,
, но это невозможно, поскольку,  и
и  . Значит
. Значит  .
.
Но так как  и
и  равноправны, то по тем же соображениям
равноправны, то по тем же соображениям  , а тогда
, а тогда  . Аналогично доказывается, что
. Аналогично доказывается, что  . Предложение доказано.
. Предложение доказано.
Предложение 6. Множество составляющих интервалов непустого ограниченного открытого множества не более, чем счетно.
Доказательство. Если каждому составляющему интервалу поставить в соответствие рациональную точку из этого интервала, то получим взаимно однозначное соответствие между составляющими интервалами и подмножеством рациональных чисел. Предложение доказано.
Объединяя последние три предложения, получим теорему.
Теорема 3. Каждое непустое ограниченное открытое множество  представимо в виде объединения конечного или счетного числа не пересекающихся составляющих интервалов
представимо в виде объединения конечного или счетного числа не пересекающихся составляющих интервалов
 ,
,  ,
,  . (4.35)
. (4.35)
Очевидно также, что всякое множество, представимое в виде объединения интервалов является открытым.
Согласно этой теореме всякое непустое ограниченное замкнутое множество  или является отрезком
или является отрезком  или же получается из отрезка удалением конечного или счетного числа взаимно не налегающих интервалов, концы которых принадлежат множеству
или же получается из отрезка удалением конечного или счетного числа взаимно не налегающих интервалов, концы которых принадлежат множеству  .
.
В качестве примера подобного построения рассмотрим к анторово множество.
На первом шаге нашего построения разделим отрезок  на три равные части, удалим интервал
на три равные части, удалим интервал  и оставшееся множество – объединение двух отрезков
и оставшееся множество – объединение двух отрезков  и
и  - обозначим через
- обозначим через 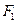 . Из этих двух отрезков в свою очередь удалим их трети: интервалы
. Из этих двух отрезков в свою очередь удалим их трети: интервалы  ,
,  . И объединение оставшихся отрезков обозначим через
. И объединение оставшихся отрезков обозначим через  . Продолжая этот процесс, получим убывающую последовательность замкнутых множеств, причем множество
. Продолжая этот процесс, получим убывающую последовательность замкнутых множеств, причем множество  является объединением
является объединением 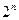 отрезков, длина каждого из которых равна
отрезков, длина каждого из которых равна 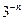 .
.
Множество
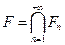
и называется канторовым множеством. Канторово множество замкнуто, как пересечение замкнутых множеств.
Канторово множество допускает эффективное описание с помощью троичных дробей. Каждое число  можно записать в виде троичной дроби
можно записать в виде троичной дроби
 ,
,
где числа  могут принимать значения 0, 1 и 2. Числа
могут принимать значения 0, 1 и 2. Числа  из интервала
из интервала  , выброшенные на первом шаге построения канторова множества, характеризуются тем, что в их троичном разложении
, выброшенные на первом шаге построения канторова множества, характеризуются тем, что в их троичном разложении  . Концы же этого интервала допускают каждый по два представления
. Концы же этого интервала допускают каждый по два представления
 ,
,  .
.
Условимся для точек канторова множества использовать такие разложения
 , в которых число 1 не встречается.
, в которых число 1 не встречается.
В результате получим взаимно однозначное соответствие между точками из канторова множества и последовательностями из цифр 0 и 2. Из такого соответствия, в частности, следует, что канторово множество имеет мощность континуума.
ЗАДАЧИ
1. Доказать, что аксиомы метрического пространства эквивалентны двум аксиомам:
1)  (аксиома тождества);
(аксиома тождества);
2) для любых трех элементов  ,
,  и
и 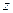
 (аксиома треугольника).
(аксиома треугольника).
2. Доказать, что для любых точек  метрического пространства справедливо неравенство
метрического пространства справедливо неравенство
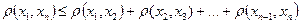 .
.
3. Является ли множество натуральных чисел 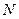 метрическим пространством, если для любых
метрическим пространством, если для любых  метрика вводится одним из соотношений:
метрика вводится одним из соотношений:
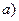
 ;
;

 ;
;
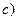
 ;
;
4. Докажите, что если 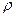 - метрика на множестве
- метрика на множестве  , то функция
, то функция
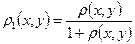
также является метрикой на  .
.
5. Будет ли метрическим пространством вещественная прямая с метрикой
 ,
,
где  -непрерывная и строго монотонная функция.
-непрерывная и строго монотонная функция.
6. Доказать, что если  - предельная точка множества
- предельная точка множества  , то в любой окрестности точки
, то в любой окрестности точки  имеется бесконечное множество точек множества
имеется бесконечное множество точек множества  .
.
7. Доказать, что если  , то
, то 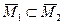 .
.
8. Доказать, что 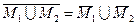 .
.
9. Доказать, что в произвольном метрическом пространстве замыкание открытого шара лежит в соответствующем замкнутом шаре:  .
.
10. Привести пример метрического пространства, в котором  .
.
11. Привести пример метрического пространства, в котором шар большего радиуса содержится в шаре меньшего радиуса.
12. Привести пример непустых и непересекающихся замкнутых множеств  и
и
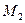 , расстояние между которыми равно нулю:
, расстояние между которыми равно нулю:  .
.
13. Доказать, что сходимость последовательности 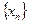 элементов пространства
элементов пространства
 к точке
к точке  означает равномерную сходимость последовательности функций
означает равномерную сходимость последовательности функций  к функции
к функции  .
.
14. Доказать, что множество  всех непрерывных на отрезке
всех непрерывных на отрезке  функций, удовлетворяющих неравенствам
функций, удовлетворяющих неравенствам  , является открытым множеством.
, является открытым множеством.
15. Пусть  - полное метрическое пространство и
- полное метрическое пространство и  . Тогда справедливы утверждения:
. Тогда справедливы утверждения:
 если множество
если множество  замкнуто, то оно полно;
замкнуто, то оно полно;
 еслимножество
еслимножество  полно, то оно замкнуто;
полно, то оно замкнуто;
16. Доказать, что прямая  с метрикой
с метрикой  не является полной. Построить пополнение этого метрического пространства.
не является полной. Построить пополнение этого метрического пространства.
17. На множестве  натуральных чисел введена метрика по формуле
натуральных чисел введена метрика по формуле
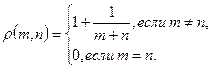
 Доказать справедливость аксиом метрического пространства,
Доказать справедливость аксиом метрического пространства,
 описать замкнутые шары
описать замкнутые шары  ,
,
 доказать, что пересечение шаров пусто:
доказать, что пересечение шаров пусто:  ,
,
 доказать полноту метрического пространства.
доказать полноту метрического пространства.
18. Докажите полноту метрического пространства  .
.
19. Докажите, что последовательность  сходится в пространстве
сходится в пространстве  .
.
20. Докажите, что последовательность  не сходится в пространстве
не сходится в пространстве  .
.
21. Доказать, что множество непрерывных на отрезке  функций с метрикой
функций с метрикой
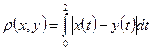
не является полным метрическим пространством.
22. Доказать, что пространство всех определенных на отрезке  многочленов с метрикой
многочленов с метрикой
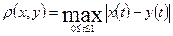
не является полным.
23. В метрическом пространстве  задана последовательность вида
задана последовательность вида
 ,
,
где ненулевых элементов ровно  . Доказать, что последовательность не сходится.
. Доказать, что последовательность не сходится.
24. Рассмотрим пространство финитных последовательностей  и для двух элементов
и для двух элементов
 ,
,  ,
,
где  , определим метрику по формуле
, определим метрику по формуле
 .
.
Найти пополнение метрического пространства  .
.
25. Докажите, что в полном метрическом пространстве замыкание относительно компактного множества является компактом.
26. Докажите, что единичный замкнутый  в пространстве
в пространстве  не является компактом.
не является компактом.
27. Докажите относительную компактность основного параллелепипеда в пространстве  , представляющего собой множество
, представляющего собой множество  точек
точек  , координаты которых удовлетворяют условиям
, координаты которых удовлетворяют условиям  ,
,  .
.
28. Докажите относительную компактность в пространстве  множества
множества  точек
точек  , координаты которых удовлетворяют условиям
, координаты которых удовлетворяют условиям  ,
,  , причем сходится ряд
, причем сходится ряд  .
.
29. Пусть множество  состоит из функций, удовлетворяющих неравенству
состоит из функций, удовлетворяющих неравенству 
 . Доказать, что множество
. Доказать, что множество  не является относительно компактным.
не является относительно компактным.
30. Пусть множество  состоит из непрерывно дифференцируемых функций, удовлетворяющих условиям
состоит из непрерывно дифференцируемых функций, удовлетворяющих условиям

 ,
,  .
.
Доказать, что множество  относительно компактно.
относительно компактно.
31. Пусть  - полное метрическое пространство,
- полное метрическое пространство,  - последовательность открытых всюду плотных множеств
- последовательность открытых всюду плотных множеств  . Докажите, что пересечение
. Докажите, что пересечение  является всюду плотным множеством.
является всюду плотным множеством.
32. Пусть 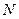 - фиксированное натуральное число и
- фиксированное натуральное число и  - множество, составленное из финитных последовательностей. Доказать, что множество
- множество, составленное из финитных последовательностей. Доказать, что множество  нигде не плотно в пространстве
нигде не плотно в пространстве  .
.
33. Докажите, что каждая точка канторова множества является его предельной точкой.
34. Докажите, что канторово множество нигде не плотно на отрезке  .
.
35. Доказать, что пространство 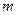 всех ограниченных числовых последовательностей
всех ограниченных числовых последовательностей  с расстоянием
с расстоянием
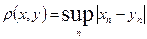
не сепарабельно.
36. Докажите, что дополнение к нигде не плотному множеству всюду плотно. Справедливо ли обратное утверждение?
37. Доказать, что дополнение к открытому всюду плотному множеству нигде не плотно.

 справедливо соотношение
справедливо соотношение . (4.23)
. (4.23) . (4.24) Доказательство. Продифференцируем по
. (4.24) Доказательство. Продифференцируем по  тождество
тождество (4.25)
(4.25) . (4.26)
. (4.26) . (4.27) Положим в (4.25), (4.26) и (4.27)
. (4.27) Положим в (4.25), (4.26) и (4.27)  и умножим полученные тождества на
и умножим полученные тождества на . В результате придем к соотношениям
. В результате придем к соотношениям , (4.29)
, (4.29) . (4.30)
. (4.30) , (4.29) на
, (4.29) на  и (4.30) на 1 и все сложим:
и (4.30) на 1 и все сложим: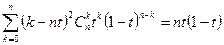 .
. , заданной на промежутке
, заданной на промежутке  многочлен
многочлен (4.31)
(4.31) , то последовательность
, то последовательность  сходится к функции
сходится к функции  , т.е. равномерно на отрезке
, т.е. равномерно на отрезке  . Вследствие равномерной непрерывности на отрезке для любого
. Вследствие равномерной непрерывности на отрезке для любого  найдется такой
найдется такой  , что если
, что если  , то
, то  .
. .
. . (4.32) Разобьем все числа
. (4.32) Разобьем все числа  на два множества
на два множества  и
и  :
: ,
,  .
. , то
, то  , и на основании утверждения 1 имеем
, и на основании утверждения 1 имеем . (4.33)
. (4.33) , то
, то  и, используя утверждение 2, получим
и, используя утверждение 2, получим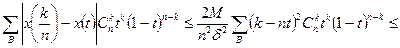
 . (4.34)
. (4.34) ,
,  .
. имеем
имеем  ,
,  . Для любого
. Для любого  , что при всех
, что при всех 
 .
. . Она определена и непрерывна на отрезке
. Она определена и непрерывна на отрезке  , что при всех
, что при всех 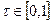
 .
. и, следовательно, справедливо неравенство
и, следовательно, справедливо неравенство .
. и является требуемым. Теорема доказана.
и является требуемым. Теорема доказана. есть самая правая точка.
есть самая правая точка. . Докажем, что всегда
. Докажем, что всегда  . По определению точней верхней грани для любого
. По определению точней верхней грани для любого  такая, что
такая, что  . Отсюда следует, что точка
. Отсюда следует, что точка  является точкой прикосновения для множества
является точкой прикосновения для множества 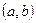 содержится во множестве
содержится во множестве  построим составляющий интервал. Положим
построим составляющий интервал. Положим  . Это множество замкнуто и ограничено снизу, а потому имеет левую точку, которую обозначим через
. Это множество замкнуто и ограничено снизу, а потому имеет левую точку, которую обозначим через  . Очевидно,
. Очевидно,  . Но
. Но  . Отсюда следует, что
. Отсюда следует, что  .
. и
и  . Последнее утверждение следует из того, что
. Последнее утверждение следует из того, что  . Далее, если
. Далее, если  и
и  , то
, то  , а это противоречит тому, что точка
, а это противоречит тому, что точка  .
. , что
, что  и
и  .
. есть составляющим интервалом множества
есть составляющим интервалом множества  . Предложение доказано.
. Предложение доказано. и
и  имеют общую точку
имеют общую точку  ,
,  . Предположим, что
. Предположим, что  . Тогда, очевидно,
. Тогда, очевидно,  , но это невозможно, поскольку,
, но это невозможно, поскольку,  и
и  . Значит
. Значит  .
. и
и  равноправны, то по тем же соображениям
равноправны, то по тем же соображениям  , а тогда
, а тогда  . Аналогично доказывается, что
. Аналогично доказывается, что  . Предложение доказано.
. Предложение доказано. ,
,  ,
,  . (4.35)
. (4.35) или же получается из отрезка удалением конечного или счетного числа взаимно не налегающих интервалов, концы которых принадлежат множеству
или же получается из отрезка удалением конечного или счетного числа взаимно не налегающих интервалов, концы которых принадлежат множеству  на три равные части, удалим интервал
на три равные части, удалим интервал  и оставшееся множество – объединение двух отрезков
и оставшееся множество – объединение двух отрезков  и
и  - обозначим через
- обозначим через 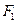 . Из этих двух отрезков в свою очередь удалим их трети: интервалы
. Из этих двух отрезков в свою очередь удалим их трети: интервалы  ,
,  . И объединение оставшихся отрезков обозначим через
. И объединение оставшихся отрезков обозначим через  . Продолжая этот процесс, получим убывающую последовательность замкнутых множеств, причем множество
. Продолжая этот процесс, получим убывающую последовательность замкнутых множеств, причем множество  является объединением
является объединением 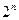 отрезков, длина каждого из которых равна
отрезков, длина каждого из которых равна 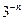 .
.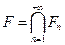
 можно записать в виде троичной дроби
можно записать в виде троичной дроби ,
, могут принимать значения 0, 1 и 2. Числа
могут принимать значения 0, 1 и 2. Числа  . Концы же этого интервала допускают каждый по два представления
. Концы же этого интервала допускают каждый по два представления ,
,  .
. , в которых число 1 не встречается.
, в которых число 1 не встречается. (аксиома тождества);
(аксиома тождества); и
и 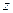
 (аксиома треугольника).
(аксиома треугольника). метрического пространства справедливо неравенство
метрического пространства справедливо неравенство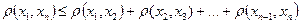 .
.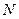 метрическим пространством, если для любых
метрическим пространством, если для любых  метрика вводится одним из соотношений:
метрика вводится одним из соотношений: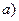
 ;
;
 ;
;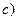
 ;
;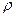 - метрика на множестве
- метрика на множестве  , то функция
, то функция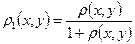
 ,
, -непрерывная и строго монотонная функция.
-непрерывная и строго монотонная функция. , то в любой окрестности точки
, то в любой окрестности точки  , то
, то 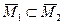 .
.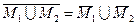 .
. .
. .
. и
и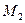 , расстояние между которыми равно нулю:
, расстояние между которыми равно нулю:  .
.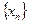 элементов пространства
элементов пространства к точке
к точке  к функции
к функции  .
. , является открытым множеством.
, является открытым множеством. . Тогда справедливы утверждения:
. Тогда справедливы утверждения: с метрикой
с метрикой  не является полной. Построить пополнение этого метрического пространства.
не является полной. Построить пополнение этого метрического пространства. натуральных чисел введена метрика по формуле
натуральных чисел введена метрика по формуле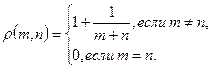
 ,
, ,
, доказать полноту метрического пространства.
доказать полноту метрического пространства. сходится в пространстве
сходится в пространстве  не сходится в пространстве
не сходится в пространстве  функций с метрикой
функций с метрикой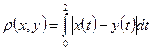
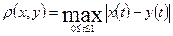
 задана последовательность вида
задана последовательность вида ,
, . Доказать, что последовательность не сходится.
. Доказать, что последовательность не сходится. и для двух элементов
и для двух элементов ,
,  ,
, , определим метрику по формуле
, определим метрику по формуле .
. в пространстве
в пространстве  не является компактом.
не является компактом. , координаты которых удовлетворяют условиям
, координаты которых удовлетворяют условиям  ,
,  .
. ,
,  .
. состоит из функций, удовлетворяющих неравенству
состоит из функций, удовлетворяющих неравенству 

 .
. - последовательность открытых всюду плотных множеств
- последовательность открытых всюду плотных множеств  . Докажите, что пересечение
. Докажите, что пересечение  является всюду плотным множеством.
является всюду плотным множеством. - множество, составленное из финитных последовательностей. Доказать, что множество
- множество, составленное из финитных последовательностей. Доказать, что множество 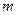 всех ограниченных числовых последовательностей
всех ограниченных числовых последовательностей  с расстоянием
с расстоянием