Теорема 3. Для того, чтобы метрическое пространство  было полным, необходимо и достаточно, чтобы в нем всякая последовательность вложенных друг в друга замкнутых шаров, радиусы которых стремятся к нулю, имела непустое пересечение.
было полным, необходимо и достаточно, чтобы в нем всякая последовательность вложенных друг в друга замкнутых шаров, радиусы которых стремятся к нулю, имела непустое пересечение.
Необходимость. Пусть пространство  полно и
полно и

последовательность вложенных друг в друга замкнутых шаров.
Последовательность центров  фундаментальна, поскольку
фундаментальна, поскольку
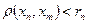 ,
,  .
.
Это неравенство следует из того, что шары вложены друг в друга. Кроме того, 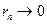 при
при 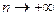 . Так как пространство
. Так как пространство  полно, то существует предел
полно, то существует предел  . Нам остается доказать, что
. Нам остается доказать, что 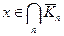 . В самом деле, шар
. В самом деле, шар  содержит все точки последовательности
содержит все точки последовательности  за исключением, быть может, конечного числа. Отсюда следует, что
за исключением, быть может, конечного числа. Отсюда следует, что  является точкой прикосновения для замкнутого шара
является точкой прикосновения для замкнутого шара  и
и  при всех
при всех 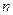 .
.
Достаточность. Нужно доказать, что всякая фундаментальная последовательность  имеет предел. В силу фундаментальности, найдется такой номер
имеет предел. В силу фундаментальности, найдется такой номер 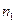 , что
, что
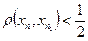 ,
, 
 .
.
Примем 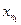 за центр замкнутого шара радиуса 1:
за центр замкнутого шара радиуса 1: 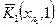 . Затем найдем
. Затем найдем  так, чтобы
так, чтобы 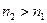 и
и
 ,
, 
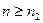 .
.
Примем 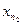 за центр замкнутого шара радиуса
за центр замкнутого шара радиуса 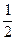 :
:  . После того, как выбраны
. После того, как выбраны 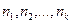 , найдем
, найдем  так, чтобы
так, чтобы
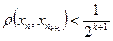 ,
, 
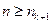 .
.
И примем  за центр замкнутого шара радиуса
за центр замкнутого шара радиуса  :
: 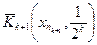 . Продолжая это построение, получим последовательность замкнутых шаров
. Продолжая это построение, получим последовательность замкнутых шаров 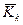 радиуса
радиуса  . Кроме того, они вложены друг в друга:
. Кроме того, они вложены друг в друга: 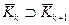 . Действительно, если
. Действительно, если  , то
, то
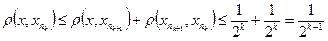 , (2.3)
, (2.3)
т.е.  . По условию теоремы последовательность шаров имеет общую точку
. По условию теоремы последовательность шаров имеет общую точку  .
.
Подпоследовательности  , как следует из (2.3), сходится к
, как следует из (2.3), сходится к  . Но тогда и вся последовательность
. Но тогда и вся последовательность  сходится к точке
сходится к точке  , как следует из предложения 3.
, как следует из предложения 3.
Теорема доказана.
Определение 6. Множество  называется нигде не плотным в метрическом пространстве
называется нигде не плотным в метрическом пространстве  , если любой открытый шар этого пространства содержит другой открытый шар, целиком свободный от точек множества
, если любой открытый шар этого пространства содержит другой открытый шар, целиком свободный от точек множества  .
.
По этому определению во всяком шаре 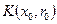 найдется другой шар
найдется другой шар  , в котором нет точек из множества
, в котором нет точек из множества  . Тогда точка
. Тогда точка  не является точкой прикосновения множества
не является точкой прикосновения множества  и поэтому не принадлежит замыканию
и поэтому не принадлежит замыканию  . Получили, что произвольный шар
. Получили, что произвольный шар 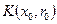 не содержится целиком в
не содержится целиком в  . Верно обратное утверждение. Если произвольный шар
. Верно обратное утверждение. Если произвольный шар 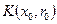 не содержится в
не содержится в  , то пересечение
, то пересечение  не пусто и открыто. Поэтому найдется открытый шар
не пусто и открыто. Поэтому найдется открытый шар  , в котором нет точек из множества
, в котором нет точек из множества  и тем более из множества
и тем более из множества  .
.
Таким образом, доказали, что определение 6 эквивалентно следующему определению.
Определение 6 (эквивалентное определение). Множество  называется нигде не плотным в метрическом пространстве
называется нигде не плотным в метрическом пространстве  , если его замыкание
, если его замыкание  не содержит ни одного открытого шара.
не содержит ни одного открытого шара.
Определение 7. Множество  называется множеством первой категории, если его можно представить в виде объединения не более, чем счетного числа нигде не плотных в
называется множеством первой категории, если его можно представить в виде объединения не более, чем счетного числа нигде не плотных в  множеств.
множеств.
Определение 8. Множество, на являющееся множеством первой категории, называется множеством второй категории.
Теорема 4 (Бэр). Полное метрическое пространство есть множество второй категории.
Доказательство. Предположим противное: 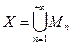 , где множества
, где множества 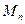 нигде не плотны. Возьмем шар
нигде не плотны. Возьмем шар  с центром в произвольной точке
с центром в произвольной точке  и радиуса 1. Поскольку множество
и радиуса 1. Поскольку множество 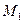 нигде не плотно, то внутри шара
нигде не плотно, то внутри шара  найдется шар
найдется шар  радиуса
радиуса  , не содержащий точек множества
, не содержащий точек множества 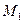 . Точно так же, внутри шара
. Точно так же, внутри шара  найдется шар
найдется шар  радиуса
радиуса  , не содержащий точек множества
, не содержащий точек множества 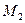 , и т.д.
, и т.д.
В результате получим последовательность вложенных замкнутых шаров 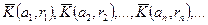 , радиусы которых стремятся к нулю. При этом шар
, радиусы которых стремятся к нулю. При этом шар  не содержит точек множеств
не содержит точек множеств  . По теореме 3, существует точка
. По теореме 3, существует точка  , принадлежащая всем шарам. Эта точка по построению не принадлежит ни одному из множеств
, принадлежащая всем шарам. Эта точка по построению не принадлежит ни одному из множеств  , следовательно,
, следовательно, 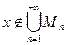 , т.е.
, т.е.  . Мы получили противоречие, которое и доказывает теорему.
. Мы получили противоречие, которое и доказывает теорему.
Определение 9. Отображение  метрического пространства
метрического пространства 
 в себя называется сжимающим, если существует такое число
в себя называется сжимающим, если существует такое число 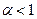 , что для любых двух точек
, что для любых двух точек  выполняется неравенство
выполняется неравенство
 . (2.4)
. (2.4)
Всякое сжимающее отображение непрерывно.
Теорема 5 (принцип сжимающих отображений). Всякое сжимающее отображение полного метрического пространства  в себя имеет одну и только одну неподвижную точку, т.е. уравнение
в себя имеет одну и только одну неподвижную точку, т.е. уравнение  имеет единственное решение
имеет единственное решение 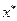 .
.
Доказательство. Возьмем произвольный элемент 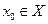 и положим
и положим
 ,
,  ,…,
,…, 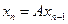 ,….
,….
Покажем, что построенная последовательность  является фундаментальной. Имеем
является фундаментальной. Имеем
 ,
,
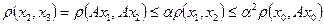 ,
,
.........................................
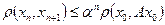 ,
,
...........................................
Далее, применяя неравенство треугольника, получим

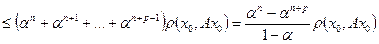 .
.
Так как, по условию 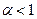 , то
, то
 ,
,
откуда следует, что  , при
, при 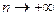 ,
, 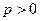 .
.
Следовательно, последовательность  фундаментальна и в силу полноты пространства
фундаментальна и в силу полноты пространства  сходится. Пусть
сходится. Пусть 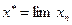 .
.
Докажем, что 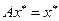 . В силу непрерывности отображения
. В силу непрерывности отображения 
 .
.
Итак, существование неподвижной точки доказано. Докажем ее единственность. Если
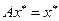 ,
,  ,
,
то неравенство (2.4) принимает вид
 ;
;
так как 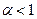 , отсюда следует, что
, отсюда следует, что
 , т.е.
, т.е. 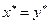 .
.
Теорема полностью доказана.

 было полным, необходимо и достаточно, чтобы в нем всякая последовательность вложенных друг в друга замкнутых шаров, радиусы которых стремятся к нулю, имела непустое пересечение.
было полным, необходимо и достаточно, чтобы в нем всякая последовательность вложенных друг в друга замкнутых шаров, радиусы которых стремятся к нулю, имела непустое пересечение.
 фундаментальна, поскольку
фундаментальна, поскольку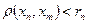 ,
,  .
.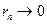 при
при 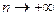 . Так как пространство
. Так как пространство  . Нам остается доказать, что
. Нам остается доказать, что 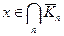 . В самом деле, шар
. В самом деле, шар  содержит все точки последовательности
содержит все точки последовательности  является точкой прикосновения для замкнутого шара
является точкой прикосновения для замкнутого шара  при всех
при всех 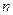 .
.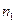 , что
, что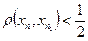 ,
, 
 .
.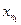 за центр замкнутого шара радиуса 1:
за центр замкнутого шара радиуса 1: 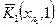 . Затем найдем
. Затем найдем  так, чтобы
так, чтобы 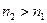 и
и ,
, 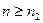 .
.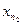 за центр замкнутого шара радиуса
за центр замкнутого шара радиуса 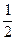 :
:  . После того, как выбраны
. После того, как выбраны 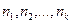 , найдем
, найдем  так, чтобы
так, чтобы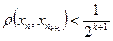 ,
, 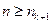 .
. за центр замкнутого шара радиуса
за центр замкнутого шара радиуса  :
: 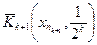 . Продолжая это построение, получим последовательность замкнутых шаров
. Продолжая это построение, получим последовательность замкнутых шаров 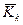 радиуса
радиуса  . Кроме того, они вложены друг в друга:
. Кроме того, они вложены друг в друга: 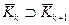 . Действительно, если
. Действительно, если  , то
, то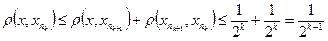 , (2.3)
, (2.3) . По условию теоремы последовательность шаров имеет общую точку
. По условию теоремы последовательность шаров имеет общую точку  , как следует из (2.3), сходится к
, как следует из (2.3), сходится к  называется нигде не плотным в метрическом пространстве
называется нигде не плотным в метрическом пространстве 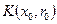 найдется другой шар
найдется другой шар  , в котором нет точек из множества
, в котором нет точек из множества  не является точкой прикосновения множества
не является точкой прикосновения множества  . Получили, что произвольный шар
. Получили, что произвольный шар  не пусто и открыто. Поэтому найдется открытый шар
не пусто и открыто. Поэтому найдется открытый шар 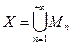 , где множества
, где множества 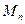 нигде не плотны. Возьмем шар
нигде не плотны. Возьмем шар  с центром в произвольной точке
с центром в произвольной точке  и радиуса 1. Поскольку множество
и радиуса 1. Поскольку множество 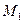 нигде не плотно, то внутри шара
нигде не плотно, то внутри шара  радиуса
радиуса  , не содержащий точек множества
, не содержащий точек множества  радиуса
радиуса  , не содержащий точек множества
, не содержащий точек множества 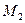 , и т.д.
, и т.д.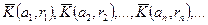 , радиусы которых стремятся к нулю. При этом шар
, радиусы которых стремятся к нулю. При этом шар  не содержит точек множеств
не содержит точек множеств  . По теореме 3, существует точка
. По теореме 3, существует точка  , принадлежащая всем шарам. Эта точка по построению не принадлежит ни одному из множеств
, принадлежащая всем шарам. Эта точка по построению не принадлежит ни одному из множеств  , следовательно,
, следовательно, 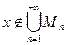 , т.е.
, т.е.  . Мы получили противоречие, которое и доказывает теорему.
. Мы получили противоречие, которое и доказывает теорему. метрического пространства
метрического пространства 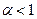 , что для любых двух точек
, что для любых двух точек  выполняется неравенство
выполняется неравенство . (2.4)
. (2.4) имеет единственное решение
имеет единственное решение 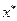 .
.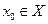 и положим
и положим ,
,  ,…,
,…, 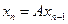 ,….
,…. ,
,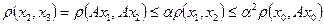 ,
,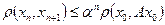 ,
,
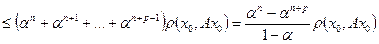 .
. ,
, , при
, при 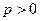 .
.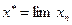 .
.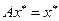 . В силу непрерывности отображения
. В силу непрерывности отображения  .
. ,
, ;
; , т.е.
, т.е. 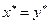 .
.


