Определение 10. Точка  метрического пространства
метрического пространства  называется пределом последовательности точек
называется пределом последовательности точек  , если
, если  , т.е. для любого положительного числа
, т.е. для любого положительного числа  найдется номер
найдется номер  такой, что при всех
такой, что при всех 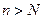 верно неравенство
верно неравенство  .
.
Записываем предел в виде  или кратко
или кратко  .
.
Используя понятие шара, дадим следующую характеристику предела: для того, чтобы  необходимо и достаточно, чтобы для любого шара
необходимо и достаточно, чтобы для любого шара  с центром в точке
с центром в точке  и радиуса
и радиуса  существовало такое
существовало такое  , что
, что  при
при 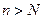 .
.
Предложение 8. Последовательность точек может иметь только один предел.
Доказательство. Пусть  и
и  . Применяя аксиому треугольника, получим
. Применяя аксиому треугольника, получим  . Правая часть этого неравенства стремится к нулю, а левая неотрицательна. Следовательно
. Правая часть этого неравенства стремится к нулю, а левая неотрицательна. Следовательно  , а тогда
, а тогда  . Предложение доказано.
. Предложение доказано.
Предложение 9. Точка  метрического пространства
метрического пространства  принадлежит замыканию
принадлежит замыканию  множества
множества  тогда и только тогда, когда существует последовательность точек
тогда и только тогда, когда существует последовательность точек  множества
множества  , сходящаяся к
, сходящаяся к  .
.
Доказательство. Пусть  . Если при этом
. Если при этом  , то в качестве последовательности можно взять
, то в качестве последовательности можно взять  . Далее полагаем, что
. Далее полагаем, что  . Тогда точка
. Тогда точка  является предельной точкой множества
является предельной точкой множества  , ему не принадлежащей. Поэтому в каждом шаре
, ему не принадлежащей. Поэтому в каждом шаре  , т.е. при любом
, т.е. при любом  , имеется хотя бы одна точка
, имеется хотя бы одна точка  . В результате построили последовательность
. В результате построили последовательность  точек из множества
точек из множества  , сходящаяся к точке
, сходящаяся к точке  .
.
Верно и обратное: если  ,
,  , то
, то  . Действительно, если
. Действительно, если  , то точка
, то точка  принадлежит открытому множеству
принадлежит открытому множеству  . Поэтому найдется открытый шар с центром в точке
. Поэтому найдется открытый шар с центром в точке  , целиком лежащий во множестве
, целиком лежащий во множестве  , т.е. не имеющий общих точек с множеством
, т.е. не имеющий общих точек с множеством  . А это противоречит тому, что последовательность точек
. А это противоречит тому, что последовательность точек  из множества
из множества  сходится к
сходится к  . Предложение доказано.
. Предложение доказано.
Предложение 10. Расстояние 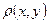 является непрерывной функцией от
является непрерывной функцией от  и
и  .
.
Доказательство. Непрерывность означает, что если  и
и 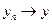 , то
, то  . Для доказательства воспользуемся неравенством (1.1). Из нее следует, что
. Для доказательства воспользуемся неравенством (1.1). Из нее следует, что
 .
.
Предложение доказано.
Предложение 11. В метрическом пространстве всякий замкнутый шар  является замкнутым множеством.
является замкнутым множеством.
Доказательство. Пусть  - произвольная предельная точка множества
- произвольная предельная точка множества  . В силу предложения 9, существует последовательность
. В силу предложения 9, существует последовательность  такая, что
такая, что  , при
, при  . Поскольку
. Поскольку  ,
,  , то, пользуясь непрерывностью расстояния и переходя к пределу в последнем неравенстве, получим неравенство
, то, пользуясь непрерывностью расстояния и переходя к пределу в последнем неравенстве, получим неравенство 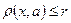 . Отсюда вытекает, что
. Отсюда вытекает, что  , т.е. этот шар содержит все свои предельные точки и поэтому является замкнутым множеством. Предложение доказано.
, т.е. этот шар содержит все свои предельные точки и поэтому является замкнутым множеством. Предложение доказано.

 метрического пространства
метрического пространства  называется пределом последовательности точек
называется пределом последовательности точек  , если
, если  , т.е. для любого положительного числа
, т.е. для любого положительного числа  найдется номер
найдется номер  такой, что при всех
такой, что при всех 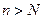 верно неравенство
верно неравенство  .
. или кратко
или кратко  .
. с центром в точке
с центром в точке  при
при  . Применяя аксиому треугольника, получим
. Применяя аксиому треугольника, получим  . Правая часть этого неравенства стремится к нулю, а левая неотрицательна. Следовательно
. Правая часть этого неравенства стремится к нулю, а левая неотрицательна. Следовательно  , а тогда
, а тогда  . Предложение доказано.
. Предложение доказано. множества
множества  тогда и только тогда, когда существует последовательность точек
тогда и только тогда, когда существует последовательность точек  множества
множества  . Если при этом
. Если при этом  , то в качестве последовательности можно взять
, то в качестве последовательности можно взять  . Далее полагаем, что
. Далее полагаем, что  . Тогда точка
. Тогда точка  , т.е. при любом
, т.е. при любом  , имеется хотя бы одна точка
, имеется хотя бы одна точка  . В результате построили последовательность
. В результате построили последовательность  точек из множества
точек из множества  ,
,  , то точка
, то точка  . Поэтому найдется открытый шар с центром в точке
. Поэтому найдется открытый шар с центром в точке 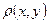 является непрерывной функцией от
является непрерывной функцией от  .
.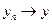 , то
, то  . Для доказательства воспользуемся неравенством (1.1). Из нее следует, что
. Для доказательства воспользуемся неравенством (1.1). Из нее следует, что .
. является замкнутым множеством.
является замкнутым множеством. такая, что
такая, что  . Поскольку
. Поскольку  ,
,  , то, пользуясь непрерывностью расстояния и переходя к пределу в последнем неравенстве, получим неравенство
, то, пользуясь непрерывностью расстояния и переходя к пределу в последнем неравенстве, получим неравенство 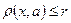 . Отсюда вытекает, что
. Отсюда вытекает, что  , т.е. этот шар содержит все свои предельные точки и поэтому является замкнутым множеством. Предложение доказано.
, т.е. этот шар содержит все свои предельные точки и поэтому является замкнутым множеством. Предложение доказано.


