Определение 2. Открытым шаром  в метрическом пространстве
в метрическом пространстве  с центром в точке
с центром в точке  и радиуса
и радиуса  называется множество всех таких точек
называется множество всех таких точек 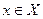 , что
, что  .
.
Замкнутым шаром  называется множество всех таких точек
называется множество всех таких точек 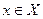 , что
, что 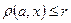 .
.
Определение 3. Множество  называется открытым в метрическом пространстве
называется открытым в метрическом пространстве  , если для любого
, если для любого  найдется такое число
найдется такое число  , что верно включение
, что верно включение  .
.
Определение 4. Окрестностью точки 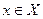 называется любое открытое множество, содержащее
называется любое открытое множество, содержащее  .
.
Предложение 2. Открытый шар является открытым множеством.
Доказательство. Покажем, что открытый шар  вместе с каждой точкой
вместе с каждой точкой  содержит шар
содержит шар  , где
, где  В самом деле, если
В самом деле, если  , то
, то
 ,
,
т.е.  . Отсюда следует доказательство предложения.
. Отсюда следует доказательство предложения.
Открытый шар является окрестностью каждой своей точки.
Предложение 3. Объединение любого числа открытых множеств открыто. Пересечение любого конечного числа открытых множеств есть открытое множество.
Доказательство. Пусть  семейство открытых в
семейство открытых в  множеств. Если
множеств. Если  , то существует такое
, то существует такое 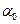 , что
, что  . Тогда найдется шар
. Тогда найдется шар  , содержащийся в
, содержащийся в 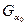 :
:  . Тем более
. Тем более  и поэтому
и поэтому 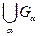 - открытое множество.
- открытое множество.
Теперь пусть имеется конечное число открытых множеств  . Если
. Если  , то для любого
, то для любого  верно включение
верно включение  . Отсюда для любого
. Отсюда для любого  найдется шар
найдется шар  , содержащийся во множестве
, содержащийся во множестве  . Взяв
. Взяв  , получим, что для любого
, получим, что для любого  справедливо включение
справедливо включение  и поэтому
и поэтому  . Это и означает, что пересечение
. Это и означает, что пересечение  - открытое множество. Предложение полностью доказано.
- открытое множество. Предложение полностью доказано.
Определение 5. Множество  в метрическом пространстве
в метрическом пространстве  называется замкнутым, если его дополнение
называется замкнутым, если его дополнение  открыто.
открыто.
Предложение 4. Пересечение любого числа замкнутых множеств замкнуто. Объединение конечного числа замкнутых множеств замкнуто.
Доказательство. По принципу двойственности дополнение объединения множеств  равно пересечению дополнений
равно пересечению дополнений 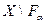 этих множеств
этих множеств

 , (1.11)
, (1.11)
а дополнение пересечения множеств  равно объединению дополнений
равно объединению дополнений 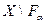 этих множеств
этих множеств
 (1.12)
(1.12)
Доказательство соотношений (1.11) и (1.12) приводится в теории множеств [1], поэтому здесь мы его не приводим. Возьмем любое число замкнутых множество  . Дополнение
. Дополнение 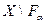 является открытым. Согласно предложения 3, объединение
является открытым. Согласно предложения 3, объединение  также будет открытым. Тогда открытым будет и левая часть (1.12). Отсюда следует, что пересечение
также будет открытым. Тогда открытым будет и левая часть (1.12). Отсюда следует, что пересечение  любого числа замкнутых множеств замкнуто.
любого числа замкнутых множеств замкнуто.
Аналогично доказывается вторая часть предложения.
Определение 6. Точка  называется точкой прикосновения множества
называется точкой прикосновения множества  , если каждая окрестность точки
, если каждая окрестность точки  содержит хотя бы одну точку множества
содержит хотя бы одну точку множества  .
.
Определение 7. Точка  называется предельной точкой множества
называется предельной точкой множества  , если каждая окрестность точки
, если каждая окрестность точки  содержит хотя бы одну точку множества
содержит хотя бы одну точку множества  , отличную от точки
, отличную от точки  .
.
Предложение 5. Множество  является замкнутым тогда и только тогда, когда оно содержит все свои токи прикосновения.
является замкнутым тогда и только тогда, когда оно содержит все свои токи прикосновения.
Доказательство. Пусть  замкнутое множество и
замкнутое множество и  его точка прикосновения. Покажем, что
его точка прикосновения. Покажем, что  . Пусть
. Пусть  , тогда
, тогда  . Множество
. Множество  является открытым, поэтому найдется окрестность точки
является открытым, поэтому найдется окрестность точки  , целиком входящая во множество
, целиком входящая во множество  . Поэтому найденная окрестность точки
. Поэтому найденная окрестность точки  не будет иметь общих точек с множеством
не будет иметь общих точек с множеством  , а это противоречит тому, что
, а это противоречит тому, что  его точка прикосновения. Полученное противоречие доказывает первую часть предложения.
его точка прикосновения. Полученное противоречие доказывает первую часть предложения.
Теперь полагаем, что множество  содержит все свои точки прикосновения; докажем, что оно замкнуто или, что дополнение
содержит все свои точки прикосновения; докажем, что оно замкнуто или, что дополнение  открыто.
открыто.
Возьмем произвольную точку  из множества
из множества  . По условию
. По условию  не является точкой прикосновения множества
не является точкой прикосновения множества  . Поэтому найдется окрестность точки
. Поэтому найдется окрестность точки  , в которой нет точек из множества
, в которой нет точек из множества  . Эта окрестность целиком лежит во множестве
. Эта окрестность целиком лежит во множестве  . Так как
. Так как  произвольная точка множества
произвольная точка множества  , то оно открыто. Предложение полностью
, то оно открыто. Предложение полностью
доказано.
Совершенно аналогично доказывается предложение.
Предложение 6. Множество  является замкнутым тогда и только тогда, когда оно содержит все свои предельные точки.
является замкнутым тогда и только тогда, когда оно содержит все свои предельные точки.
Определение 8. Множество всех точек прикосновения множества  называется замыканием множества
называется замыканием множества  и обозначается символом
и обозначается символом  .
.
Предложение 7. Имеет место соотношение  .
.
Доказательство. Надо доказать, что  . Пусть
. Пусть  . Возьмем произвольную окрестность
. Возьмем произвольную окрестность  точки
точки  . Пересечение
. Пересечение 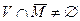 ; пусть
; пусть  . Так как
. Так как  , а
, а  является окрестностью точки
является окрестностью точки  , то
, то  . Поскольку
. Поскольку  - произвольная окрестность точки
- произвольная окрестность точки  , то получаем, что
, то получаем, что  . Предложение доказано.
. Предложение доказано.
Отсюда с учетом предложения 5 имеем.
Следствие. Множество  замкнуто.
замкнуто.
Дадим еще одно важное определение.
Определение 9. Точка  , принадлежащая
, принадлежащая  ,называется изолированной точкой этого множества, если в некоторой ее окрестности нет точек из
,называется изолированной точкой этого множества, если в некоторой ее окрестности нет точек из  , отличных от
, отличных от  .
.
Всякая точка прикосновения множества  , как следует из определений, является либо предельной точкой для него, либо изолированной точкой этого множества. Отсюда следует, что замыкание
, как следует из определений, является либо предельной точкой для него, либо изолированной точкой этого множества. Отсюда следует, что замыкание  множества
множества  состоит из точек трех типов:
состоит из точек трех типов:
1) изолированные точки  ;
;
2) предельные точки множества  , принадлежащие
, принадлежащие  ;
;
3) предельные точки множества  , не принадлежащие
, не принадлежащие  .
.
Следовательно, замыкание  множества
множества  получается присоединением к
получается присоединением к  всех его предельных точек.
всех его предельных точек.

 в метрическом пространстве
в метрическом пространстве  с центром в точке
с центром в точке  и радиуса
и радиуса  называется множество всех таких точек
называется множество всех таких точек 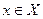 , что
, что  .
. называется множество всех таких точек
называется множество всех таких точек 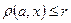 .
. называется открытым в метрическом пространстве
называется открытым в метрическом пространстве  найдется такое число
найдется такое число  , что верно включение
, что верно включение  .
. .
. , где
, где  В самом деле, если
В самом деле, если  , то
, то ,
, . Отсюда следует доказательство предложения.
. Отсюда следует доказательство предложения. семейство открытых в
семейство открытых в  , то существует такое
, то существует такое 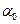 , что
, что  . Тогда найдется шар
. Тогда найдется шар  , содержащийся в
, содержащийся в 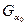 :
:  . Тем более
. Тем более  и поэтому
и поэтому 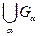 - открытое множество.
- открытое множество. . Если
. Если  , то для любого
, то для любого  верно включение
верно включение  . Отсюда для любого
. Отсюда для любого  найдется шар
найдется шар  , содержащийся во множестве
, содержащийся во множестве  . Взяв
. Взяв  , получим, что для любого
, получим, что для любого  и поэтому
и поэтому  . Это и означает, что пересечение
. Это и означает, что пересечение  в метрическом пространстве
в метрическом пространстве  открыто.
открыто. равно пересечению дополнений
равно пересечению дополнений 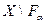 этих множеств
этих множеств
 , (1.11)
, (1.11) (1.12)
(1.12) также будет открытым. Тогда открытым будет и левая часть (1.12). Отсюда следует, что пересечение
также будет открытым. Тогда открытым будет и левая часть (1.12). Отсюда следует, что пересечение  любого числа замкнутых множеств замкнуто.
любого числа замкнутых множеств замкнуто. . Пусть
. Пусть  , тогда
, тогда  . Множество
. Множество  .
. .
. . Пусть
. Пусть  . Возьмем произвольную окрестность
. Возьмем произвольную окрестность  точки
точки 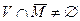 ; пусть
; пусть  . Так как
. Так как  , а
, а  , то
, то  . Поскольку
. Поскольку  . Предложение доказано.
. Предложение доказано.


