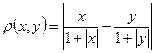Пусть  и
и  - два метрических пространства и
- два метрических пространства и 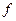 - некоторое отображение
- некоторое отображение  в
в  , которое каждому элементу
, которое каждому элементу 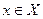 ставит в соответствие некоторый элемент
ставит в соответствие некоторый элемент 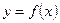 .
.
Определение 11. Отображение 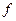 называется непрерывным в точке
называется непрерывным в точке  , если
, если
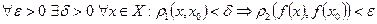 . (1.13)
. (1.13)
Если отображение 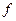 непрерывно в каждой точке пространства
непрерывно в каждой точке пространства  , то его называют непрерывным на
, то его называют непрерывным на  . Справедлива теорема.
. Справедлива теорема.
Теорема 1. Отображение 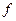 непрерывно в точке
непрерывно в точке  тогда и только тогда, когда для любой последовательности
тогда и только тогда, когда для любой последовательности  , сходящейся к
, сходящейся к  , последовательность
, последовательность  сходится к
сходится к  .
.
Доказательство. Пусть 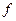 непрерывно в точке
непрерывно в точке  и
и  . По
. По  найдем такое
найдем такое 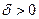 , чтобы из неравенства
, чтобы из неравенства  следовало
следовало  . А для
. А для  найдем число
найдем число  такое, при
такое, при 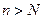 выполнено
выполнено 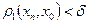 . Тогда
. Тогда  и, следовательно,
и, следовательно, 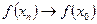 .
.
Докажем обратное. Пусть для любой последовательности  имеем
имеем 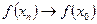 , но отображение
, но отображение 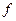 не является непрерывным. Построим в символьной форме отрицание (1.13)
не является непрерывным. Построим в символьной форме отрицание (1.13)
 . (1.14)
. (1.14)
На основе (1.14) выберем  так, что
так, что  , но
, но  . Тогда
. Тогда  , но
, но  не сходится к
не сходится к  . Полученное противоречие и доказывает вторую часть теоремы.
. Полученное противоречие и доказывает вторую часть теоремы.
Определение 12. Взаимно однозначное отображение 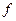 пространства
пространства  на все пространство
на все пространство  , для которого обратное отображение также непрерывно, называется гомеоморфным отображением или гомеоморфизмом. При этом соответствующие пространства
, для которого обратное отображение также непрерывно, называется гомеоморфным отображением или гомеоморфизмом. При этом соответствующие пространства  и
и  называются гомеоморфными.
называются гомеоморфными.
Примером гомеоморфизма является функция  , отображающая прямую
, отображающая прямую  на интервал
на интервал  .
.
Определение 13. Отображение 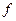 называется равномерно непрерывным, если
называется равномерно непрерывным, если
 . (1.15)
. (1.15)
Каждое равномерно непрерывное отображение непрерывно, но обратное неверно. Как доказывается в курсе математического анализа, на действительной прямой функция  не является равномерно непрерывной.
не является равномерно непрерывной.
Определение 14. Отображение 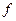 , действующее в метрическом пространстве
, действующее в метрическом пространстве  удовлетворяет условию Гельдера порядка
удовлетворяет условию Гельдера порядка 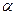 ,
, 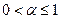 , если существует такая постоянная
, если существует такая постоянная 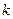 , что при всех
, что при всех  выполнено неравенство
выполнено неравенство
 .
.
При  говорят, что
говорят, что 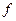 удовлетворяет условию Липшица.
удовлетворяет условию Липшица.
Функция, удовлетворяющая условию Гельдера порядка 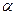 равномерно непрерывна, но обратное неверно, как показывает следующий пример:
равномерно непрерывна, но обратное неверно, как показывает следующий пример:
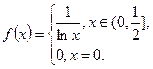
Приведем еще одно определение, которое играет очень важную роль в теории метрических пространств.
Определение 15. Отображение 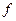 метрического пространства
метрического пространства  в метрическое пространство
в метрическое пространство  называется изометрическим (изометрией), если для любых
называется изометрическим (изометрией), если для любых  выполнено равенство
выполнено равенство
 . (1.16)
. (1.16)
Изометрическое отображение пространства  на все пространство
на все пространство  называется изометрическим изоморфизмом, a пространства
называется изометрическим изоморфизмом, a пространства  и
и  называются изометричными.
называются изометричными.
С точки зрения теории метрических пространств изометричные пространства считаются одинаковыми.
Приведем пример такого отображения. Прямая  с метрикой
с метрикой
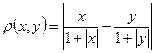
изометрична интервалу  с обычной метрикой. Изометрия задается отображением
с обычной метрикой. Изометрия задается отображением


 и
и  - два метрических пространства и
- два метрических пространства и 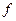 - некоторое отображение
- некоторое отображение  в
в  , которое каждому элементу
, которое каждому элементу 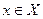 ставит в соответствие некоторый элемент
ставит в соответствие некоторый элемент 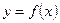 .
. , если
, если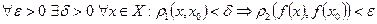 . (1.13)
. (1.13) тогда и только тогда, когда для любой последовательности
тогда и только тогда, когда для любой последовательности  , сходящейся к
, сходящейся к  сходится к
сходится к  .
. . По
. По  найдем такое
найдем такое 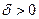 , чтобы из неравенства
, чтобы из неравенства  следовало
следовало  . А для
. А для  найдем число
найдем число  такое, при
такое, при 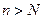 выполнено
выполнено 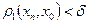 . Тогда
. Тогда  и, следовательно,
и, следовательно, 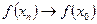 .
. . (1.14)
. (1.14) , но
, но  . Тогда
. Тогда  , отображающая прямую
, отображающая прямую  на интервал
на интервал  .
. . (1.15)
. (1.15) не является равномерно непрерывной.
не является равномерно непрерывной.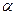 ,
, 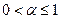 , если существует такая постоянная
, если существует такая постоянная 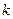 , что при всех
, что при всех  выполнено неравенство
выполнено неравенство .
. говорят, что
говорят, что 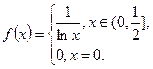
 выполнено равенство
выполнено равенство . (1.16)
. (1.16)