Примеры неполных пространств
Определение 1. Последовательность точек Предложение 1. Если последовательность Доказательство. Пусть Обратное утверждение, вообще говоря, неверно. Прежде, чем привести соответствующие примеры, изучим свойство фундаментальных последовательностей. Определение 2. Подмножество метрического пространства называется ограниченным, если оно содержится в некотором шаре. Предложение 2. Фундаментальная последовательность ограничена. Доказательство. Из определения фундаментальной последовательности следует существование такого
Пример 1. Пусть Рассмотрим последовательность Пример 2. На прямой
Все аксиомы метрического пространства выполнены. Последовательность
Однако эта последовательность не имеет предела, поскольку для любого Определение 3. Метрическое пространство Метрические пространства в примерах 1 и 2 не являются полными. Однако произвольное метрическое пространство можно включить некоторым способом в полное метрическое пространство. И доказательству этого положения посвящен следующий параграф. А в заключение этого параграфа приведем предложение, которое часто используется при доказательствах. Предложение 3. Если фундаментальная последовательность Доказательство. Так как
Поскольку
|

 метрического пространства
метрического пространства  называется фундаментальной или последовательностью Коши, если для любого
называется фундаментальной или последовательностью Коши, если для любого 
 найдется номер
найдется номер  такой, что
такой, что  при
при  .
. сходится к пределу
сходится к пределу  , то она является фундаментальной или последовательностью Коши.
, то она является фундаментальной или последовательностью Коши. . Тогда для любого
. Тогда для любого  при
при  . Следовательно,
. Следовательно,  для
для  верно неравенство
верно неравенство  . Тогда все
. Тогда все  содержатся в шаре
содержатся в шаре  и, далее, уже все элементы последовательности
и, далее, уже все элементы последовательности  , где
, где .
.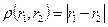 . В результате
. В результате  . Эта последовательность является фундаментальной. Но она не имеет предела в
. Эта последовательность является фундаментальной. Но она не имеет предела в  не является рациональным числом.
не является рациональным числом. введем расстояние
введем расстояние .
. является фундаментальной, поскольку
является фундаментальной, поскольку при
при  .
. имеет место соотношение
имеет место соотношение 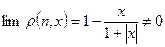 .
. , сходящуюся к точке
, сходящуюся к точке  .
. имеем
имеем .
. , то, переходя к пределу в последнем неравенстве к пределу, получаем, что
, то, переходя к пределу в последнем неравенстве к пределу, получаем, что  . Это и означает, что
. Это и означает, что 


