Определение 1. Метрическое пространство  называется компактным, если у любой последовательности точек этого пространства существует сходящаяся подпоследовательность.
называется компактным, если у любой последовательности точек этого пространства существует сходящаяся подпоследовательность.
Предложение 1. Метрическое пространство  компактно тогда и только тогда, когда каждое бесконечное подмножество имеет хотя бы одну предельную точку.
компактно тогда и только тогда, когда каждое бесконечное подмножество имеет хотя бы одну предельную точку.
Необходимость. Если  содержит бесконечное множество точек пространства
содержит бесконечное множество точек пространства  , то в нем можно взять счетное множество
, то в нем можно взять счетное множество 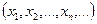 различных точек. По условию теоремы эта последовательность имеет подпоследовательность, которая сходится к некоторой точке
различных точек. По условию теоремы эта последовательность имеет подпоследовательность, которая сходится к некоторой точке  . Тогда точка
. Тогда точка  и будет предельной для множества
и будет предельной для множества  .
.
Достаточность. Пусть  последовательность точек пространства
последовательность точек пространства  . Обозначим через
. Обозначим через  множество ее членов. Если множество
множество ее членов. Если множество  конечно, то последовательность
конечно, то последовательность  содержит подпоследовательность с совпадающими элементами (стационарную), которая сходится. Если же
содержит подпоследовательность с совпадающими элементами (стационарную), которая сходится. Если же  бесконечно, то у него есть предельная точка
бесконечно, то у него есть предельная точка  . Поэтому найдется целое число
. Поэтому найдется целое число 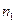 такое, что
такое, что  . Выберем затем такое число
. Выберем затем такое число  , что
, что 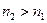 и
и  , затем найдем такое целое число
, затем найдем такое целое число  , что
, что  . Продолжая процесс, мы построим подпоследовательность
. Продолжая процесс, мы построим подпоследовательность  такую, что
такую, что  . Отсюда следует, что построенная подпоследовательность сходится к
. Отсюда следует, что построенная подпоследовательность сходится к  . Предложение доказано.
. Предложение доказано.
Предложение 2. Компактное метрическое пространство полно.
Доказательство. Пусть  - фундаментальная последовательность в компактном пространстве
- фундаментальная последовательность в компактном пространстве  . У нее существует подпоследовательность
. У нее существует подпоследовательность  , сходящаяся к некоторой точке
, сходящаяся к некоторой точке  . Тогда, согласно предложения 3 из второй главы,
. Тогда, согласно предложения 3 из второй главы,  . Предложение доказано.
. Предложение доказано.
Обратное утверждение неверно. Прямая, с обычной метрикой – полно, но не компактно.
Определение 2. Метрическое пространство  называется относительно компактным, если у любой последовательности точек этого пространства существует фундаментальная подпоследовательность.
называется относительно компактным, если у любой последовательности точек этого пространства существует фундаментальная подпоследовательность.
Из предложения 2 следует
Предложение 3. Метрическое пространство  компактно тогда и только тогда, когда оно относительно компактно и полно.
компактно тогда и только тогда, когда оно относительно компактно и полно.
Определение 3. Множество  метрического пространства
метрического пространства  называется компактным, если у любой последовательности точек этого множества существует сходящаяся
называется компактным, если у любой последовательности точек этого множества существует сходящаяся  подпоследовательность.
подпоследовательность.
Определение 4. Множество  метрического пространства
метрического пространства  называется относительно компактным, если у любой последовательности точек этого множества существует фундаментальная подпоследовательность.
называется относительно компактным, если у любой последовательности точек этого множества существует фундаментальная подпоследовательность.
Предложение 4. Относительно компактное множество ограничено.
Докажем от противного. Пусть относительно компактное множество  не ограничено. Возьмем любую его точку
не ограничено. Возьмем любую его точку  и положим
и положим  . Поскольку
. Поскольку  не ограничено, то в нем найдется такая точка
не ограничено, то в нем найдется такая точка  , что
, что  . Положим
. Положим  . Множество
. Множество  не может содержаться в шаре
не может содержаться в шаре  , поэтому в
, поэтому в  найдется точка
найдется точка  такая, что
такая, что  . Полагаем
. Полагаем  и продолжаем этот процесс до бесконечности. В результате получим последовательность точек
и продолжаем этот процесс до бесконечности. В результате получим последовательность точек  и возрастающую последовательность чисел
и возрастающую последовательность чисел  .
.
При всех 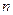 , по построению, выполняется неравенство
, по построению, выполняется неравенство
 .
.
Отсюда при любых  имеем
имеем
 . (3.2)
. (3.2)
Далее из неравенства треугольника

с учетом неравенства (3.2) и соотношений  ,
, 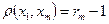 получаем окончательно неравенство
получаем окончательно неравенство
 . (3.3)
. (3.3)
Как следует из определения, никакая подпоследовательность, выделенная из  , не может быть фундаментальной. Полученное противоречие доказывает предложение.
, не может быть фундаментальной. Полученное противоречие доказывает предложение.
Определение 5. Пусть  и
и  подмножество метрического пространства
подмножество метрического пространства  . Множество
. Множество  называется
называется 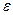 - сетью для множества
- сетью для множества  , если для любой точки
, если для любой точки 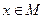 существует точка
существует точка 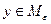 такая, что
такая, что  .
.
Геометрически это определение означает, что множество  содержится в объединении шаров радиуса
содержится в объединении шаров радиуса 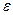 с центрами в точках множества
с центрами в точках множества  .
.
Определение 6. Множество 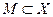 называется вполне ограниченным, если для любого
называется вполне ограниченным, если для любого  в
в  существует конечная
существует конечная 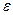 - сеть для
- сеть для  .
.
Вполне ограниченное множество может быть покрыто конечным числом шаров с произвольным заданным радиусом  . Важное место занимает теорема.
. Важное место занимает теорема.
Теорема 1 (Хаусдорф). Метрическое пространство относительно компактно тогда и только тогда, когда оно вполне ограничено.
Необходимость докажем от противного. Пусть для пространства  при некотором
при некотором  не существует
не существует 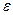 - сети. Возьмем произвольную точку
- сети. Возьмем произвольную точку  . Множество
. Множество  , состоящее из одного элемента, не образует
, состоящее из одного элемента, не образует 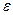 - сеть для
- сеть для  . Поэтому найдется точка
. Поэтому найдется точка  такая, что
такая, что  .
.
Множество  также не образует
также не образует 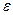 - сеть для
- сеть для  , следовательно, найдется
, следовательно, найдется  , причем
, причем  ,
,  . Продолжая этот процесс, мы построим последовательность
. Продолжая этот процесс, мы построим последовательность  такую, что
такую, что
 ,
,  ,
,  .
.
Из этой последовательности нельзя выделить фундаментальную подпоследовательность, что противоречит относительной компактности  .
.
Достаточность. Пусть  вполне ограничено и
вполне ограничено и  - произвольная последовательность. Возьмем последовательность чисел
- произвольная последовательность. Возьмем последовательность чисел  ,
,  . Построим конечную
. Построим конечную  - сеть для
- сеть для  , т.е. покроем
, т.е. покроем  конечным числом шаров радиуса
конечным числом шаров радиуса  . В один из этих шаров попадет бесконечная подпоследовательность
. В один из этих шаров попадет бесконечная подпоследовательность  последовательности
последовательности  . Из членов этой подпоследовательности выберем
. Из членов этой подпоследовательности выберем 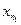 с наименьшим номером. Далее построим конечную
с наименьшим номером. Далее построим конечную  - сеть для
- сеть для  . В один из построенных шаров попадет бесконечная подпоследовательность
. В один из построенных шаров попадет бесконечная подпоследовательность 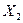 из
из  . Выберем
. Выберем 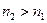 и элемент
и элемент  . Продолжая этот процесс бесконечно, мы построим подпоследовательность
. Продолжая этот процесс бесконечно, мы построим подпоследовательность  . При
. При  точки
точки  и
и  принадлежат одному шару радиуса
принадлежат одному шару радиуса  и с центром, например, в точке
и с центром, например, в точке  . Из неравенства треугольника имеем
. Из неравенства треугольника имеем
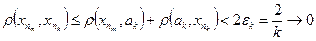 , при
, при  ,
,
т.е.  - фундаментальная последовательность. Теорема полностью доказана.
- фундаментальная последовательность. Теорема полностью доказана.
Из теоремы Хаусдорфа и предложения 3 следует следствие.
Следствие 1. Если пространство  полно и вполне ограничено, то оно компактно.
полно и вполне ограничено, то оно компактно.
Следствие 2. Множество  является относительно компактным, если для любого
является относительно компактным, если для любого  существует относительно компактная
существует относительно компактная 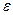 - сеть.
- сеть.
Доказательство. Пусть 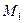 - относительно компактная
- относительно компактная  -сеть для
-сеть для  . По теореме Хаусдорфа для
. По теореме Хаусдорфа для 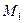 существует конечная
существует конечная  -сеть
-сеть 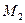 . Возьмем
. Возьмем 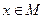 . Существует такая точка
. Существует такая точка  , что
, что  , а для
, а для  существует точка
существует точка  такая, что
такая, что  . Тогда
. Тогда  и, следовательно, множество
и, следовательно, множество 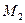 является конечной
является конечной 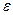 - сетью для множества. Следствие доказано.
- сетью для множества. Следствие доказано.
Определение 7. Метрическое пространство называется сепарабельным, если в нем существует счетное или конечное всюду плотное подмножество.
Следствие 3. Относительно компактное пространство  сепарабельно.
сепарабельно.
Доказательство. Пусть  ,
,  и множество
и множество 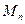 является конечной
является конечной  - сетью для пространства
- сетью для пространства  . Множество
. Множество  счетно и в то же время всюду плотно в
счетно и в то же время всюду плотно в  . Действительно, для любого
. Действительно, для любого  и
и  можно найти число
можно найти число 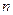 такое, что
такое, что  , и точку
, и точку  такую, что
такую, что  . Таким образом,
. Таким образом, 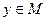 и
и  ; множество
; множество  всюду плотно в
всюду плотно в  . Следствие доказано.
. Следствие доказано.
Предложение 5. Пусть дана последовательность  непустых компактных множеств метрического пространства
непустых компактных множеств метрического пространства  Тогда пересечение
Тогда пересечение  не пусто.
не пусто.
Доказательство. В каждом множестве  выберем точку
выберем точку 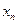 и построим последовательность
и построим последовательность  . Она содержится в компактном множестве
. Она содержится в компактном множестве  и поэтому из нее можно выделить подпоследовательность
и поэтому из нее можно выделить подпоследовательность  , которая сходится к некоторой точке
, которая сходится к некоторой точке  .
.
При любом фиксированном 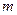 , начиная с номера
, начиная с номера  все члены последовательности
все члены последовательности  принадлежат
принадлежат  и
и  замкнуто. Отсюда следует, что
замкнуто. Отсюда следует, что  , но тогда
, но тогда  . Предложение доказано.
. Предложение доказано.

 называется компактным, если у любой последовательности точек этого пространства существует сходящаяся подпоследовательность.
называется компактным, если у любой последовательности точек этого пространства существует сходящаяся подпоследовательность. содержит бесконечное множество точек пространства
содержит бесконечное множество точек пространства 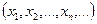 различных точек. По условию теоремы эта последовательность имеет подпоследовательность, которая сходится к некоторой точке
различных точек. По условию теоремы эта последовательность имеет подпоследовательность, которая сходится к некоторой точке  . Тогда точка
. Тогда точка  последовательность точек пространства
последовательность точек пространства 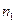 такое, что
такое, что  . Выберем затем такое число
. Выберем затем такое число  , что
, что 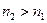 и
и  , затем найдем такое целое число
, затем найдем такое целое число  , что
, что  . Продолжая процесс, мы построим подпоследовательность
. Продолжая процесс, мы построим подпоследовательность  такую, что
такую, что  . Отсюда следует, что построенная подпоследовательность сходится к
. Отсюда следует, что построенная подпоследовательность сходится к  . Предложение доказано.
. Предложение доказано. метрического пространства
метрического пространства  и положим
и положим  . Поскольку
. Поскольку  , что
, что  . Положим
. Положим  . Множество
. Множество  , поэтому в
, поэтому в  такая, что
такая, что  . Полагаем
. Полагаем  и продолжаем этот процесс до бесконечности. В результате получим последовательность точек
и продолжаем этот процесс до бесконечности. В результате получим последовательность точек  и возрастающую последовательность чисел
и возрастающую последовательность чисел  .
.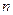 , по построению, выполняется неравенство
, по построению, выполняется неравенство .
. имеем
имеем . (3.2)
. (3.2)
 ,
, 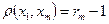 получаем окончательно неравенство
получаем окончательно неравенство . (3.3)
. (3.3) , не может быть фундаментальной. Полученное противоречие доказывает предложение.
, не может быть фундаментальной. Полученное противоречие доказывает предложение. и
и  называется
называется 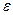 - сетью для множества
- сетью для множества 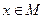 существует точка
существует точка 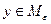 такая, что
такая, что  .
.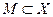 называется вполне ограниченным, если для любого
называется вполне ограниченным, если для любого  . Множество
. Множество  , состоящее из одного элемента, не образует
, состоящее из одного элемента, не образует  такая, что
такая, что  .
. также не образует
также не образует  , причем
, причем  ,
,  . Продолжая этот процесс, мы построим последовательность
. Продолжая этот процесс, мы построим последовательность  ,
,  ,
,  .
. - произвольная последовательность. Возьмем последовательность чисел
- произвольная последовательность. Возьмем последовательность чисел  ,
,  . Построим конечную
. Построим конечную  - сеть для
- сеть для  последовательности
последовательности 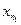 с наименьшим номером. Далее построим конечную
с наименьшим номером. Далее построим конечную  - сеть для
- сеть для 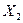 из
из  . Продолжая этот процесс бесконечно, мы построим подпоследовательность
. Продолжая этот процесс бесконечно, мы построим подпоследовательность  . При
. При  точки
точки  и
и  принадлежат одному шару радиуса
принадлежат одному шару радиуса  и с центром, например, в точке
и с центром, например, в точке  . Из неравенства треугольника имеем
. Из неравенства треугольника имеем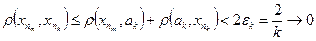 , при
, при  ,
, является относительно компактным, если для любого
является относительно компактным, если для любого 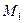 - относительно компактная
- относительно компактная  -сеть для
-сеть для 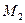 . Возьмем
. Возьмем  , что
, что  , а для
, а для  существует точка
существует точка  такая, что
такая, что  . Тогда
. Тогда  и, следовательно, множество
и, следовательно, множество 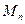 является конечной
является конечной  - сетью для пространства
- сетью для пространства  счетно и в то же время всюду плотно в
счетно и в то же время всюду плотно в  и
и  , и точку
, и точку  такую, что
такую, что  . Таким образом,
. Таким образом, 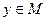 и
и  ; множество
; множество  непустых компактных множеств метрического пространства
непустых компактных множеств метрического пространства  Тогда пересечение
Тогда пересечение  не пусто.
не пусто. выберем точку
выберем точку 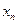 и построим последовательность
и построим последовательность  и поэтому из нее можно выделить подпоследовательность
и поэтому из нее можно выделить подпоследовательность  .
.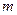 , начиная с номера
, начиная с номера  все члены последовательности
все члены последовательности  и
и  , но тогда
, но тогда  . Предложение доказано.
. Предложение доказано.


