Примеры метрических пространств
Приведем примеры наиболее часто встречающихся метрических пространств. При этом первые две аксиомы проверяются без труда. Для проверки аксиомы треугольника в ряде случаев используются известные неравенства, имеющие самостоятельное значение. Доказательство таких неравенств, как правило, приводится в приложении. 1. Пространство изолированных точек (или дискретное метрическое пространство) - это произвольное множество, для которого
Все три аксиомы очевидно выполняются. 2. Множество действительных чисел с расстоянием
образует метрическое пространство 3. Во множестве действительных чисел метрику можно также определить по формуле
Здесь 4. Евклидово пространство
Пусть
Полагая
Это – так называемое неравенство Минковского. Его доказательство приводится в приложении. 5. Пространство
Проверим аксиому треугольника. Имеем
Отсюда
6. Пространство
Неравенство треугольника проверяется с помощью неравенства Минковского, приводимого в приложении. 7. Пространство
Этот ряд, очевидно, сходится. Для проверки неравенства треугольника, вначале докажем одно вспомогательное неравенство. Пусть
Возьмем три последовательности
Умножая крайние члены ряда (1.9) на 8. Пространство
Проверим аксиому треугольника. Имеем
Так как неравенство (1.10) справедливо при всех
9. Пространство
где Расстояние в этом пространстве определяется по формуле
Неравенство треугольника проверяется с помощью неравенства Минковского для интегралов, приводимого в приложении. 10. В заключении приведем еще одно пространство. На действительной прямой
Аксиомы метрического пространства проверяются без труда.
|

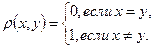

 .
.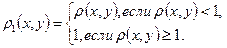
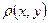 определяется как в примере 2.
определяется как в примере 2.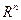 - это множество упорядоченных наборов из
- это множество упорядоченных наборов из  действительных чисел
действительных чисел 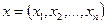 с расстоянием
с расстоянием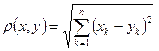 (
(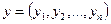 ) (1.5)
) (1.5) ; тогда аксиома треугольника записывается в виде
; тогда аксиома треугольника записывается в виде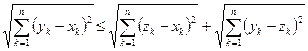 . (1.6)
. (1.6)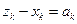 ,
, 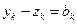 , получаем
, получаем  , а неравенство (1.6) принимает вид
, а неравенство (1.6) принимает вид . (1.7)
. (1.7)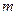 всех ограниченных числовых последовательностей
всех ограниченных числовых последовательностей 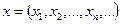 . Последовательность
. Последовательность  ограничена, если найдется такое число
ограничена, если найдется такое число 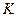 , что верно неравенство
, что верно неравенство 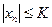 для всех
для всех  расстояние определяется по формуле
расстояние определяется по формуле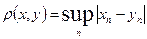 .
.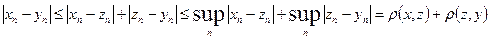 .
.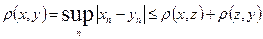 .
.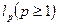 состоит из вещественных последовательностей
состоит из вещественных последовательностей  . Расстояние в нем определяется по формуле
. Расстояние в нем определяется по формуле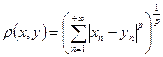 .
. всех числовых последовательностей. Метрику в нем определяем по формуле
всех числовых последовательностей. Метрику в нем определяем по формуле .
.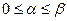 . Тогда
. Тогда  . Деля это неравенство на
. Деля это неравенство на 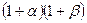 , получим
, получим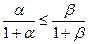 . (1.8)
. (1.8)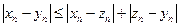 и с учетом (1.8) имеем
и с учетом (1.8) имеем
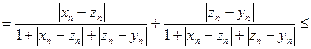
 . (1.9)
. (1.9)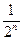 и суммируя по
и суммируя по  всех непрерывных действительных функций
всех непрерывных действительных функций  , определенных на отрезке
, определенных на отрезке 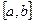 , с расстоянием
, с расстоянием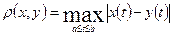 .
.
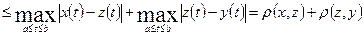 . (1.10)
. (1.10)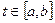 , то получим
, то получим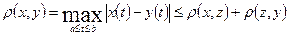 . Следовательно
. Следовательно 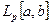 состоит из всех измеримых по Лебегу на
состоит из всех измеримых по Лебегу на 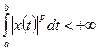 ,
,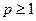 - некоторое положительное число.
- некоторое положительное число. .
. определим метрику с помощью строго монотонной действительной функции
определим метрику с помощью строго монотонной действительной функции 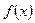 , полагая
, полагая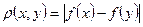 .
.


