Рассмотрим кубируемую область в трехмерном пространстве  . Разбиение
. Разбиение  на части
на части  осуществляется непрерывными поверхностями. Диаметр разбиения определяется аналогично двумерному случаю. Также, по аналогии, можно определить для функции
осуществляется непрерывными поверхностями. Диаметр разбиения определяется аналогично двумерному случаю. Также, по аналогии, можно определить для функции  , разбиения
, разбиения  области
области  и выбранных точек
и выбранных точек  интегральную сумму
интегральную сумму  , где
, где  обозначает объем области
обозначает объем области  .
.
Определение. Пусть  такое число, что
такое число, что 
 . Тогда мы говорим, что
. Тогда мы говорим, что  интегрируема на
интегрируема на  , число
, число  есть интеграл
есть интеграл  по области
по области  и обозначаем это так:
и обозначаем это так: 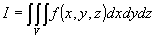 .
.
Как и в случае двойного интеграла, выполняются аналогичные свойства 1-6. Можно доказать, что если  непрерывна на
непрерывна на  , то она интегрируема на
, то она интегрируема на  . Точно также можно убедиться в том, что если точки разрыва
. Точно также можно убедиться в том, что если точки разрыва  лежат на конечном числе непрерывных поверхностей, лежащих в
лежат на конечном числе непрерывных поверхностей, лежащих в  и разбивающих
и разбивающих  на кубируемые области, то
на кубируемые области, то  интегрируема на
интегрируема на  .
.
Вычисление тройного интеграла производится по следующему правилу.
Теорема. Пусть  задана следующими неравенствами:
задана следующими неравенствами: 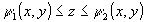 ,
, 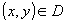 .
.  - квадрируемая область на плоскости,
- квадрируемая область на плоскости,  - непрерывные. Тогда
- непрерывные. Тогда 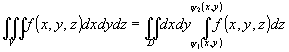
Замечание. Если область  задана неравенствами
задана неравенствами  , где
, где  - непрерывные функции, то
- непрерывные функции, то 
Сформулируем общую теорему о замене переменных.
Теорема. Пусть отображение  устанавливает взаимно однозначное соответствие между областями
устанавливает взаимно однозначное соответствие между областями  и
и 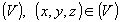 , причем функции
, причем функции  - непрерывно дифференцируемые и
- непрерывно дифференцируемые и  ни в одной точке
ни в одной точке  . Пусть
. Пусть  - непрерывная на
- непрерывная на  функция. Тогда
функция. Тогда 
Как и для двойного интеграла, теорема остается верна в случае нарушения ее условий на множестве нулевого объема.
13 Трехкратный интеграл и его свойства (есть)
14 Криволинейный интеграл

 . Разбиение
. Разбиение  на части
на части  осуществляется непрерывными поверхностями. Диаметр разбиения определяется аналогично двумерному случаю. Также, по аналогии, можно определить для функции
осуществляется непрерывными поверхностями. Диаметр разбиения определяется аналогично двумерному случаю. Также, по аналогии, можно определить для функции  , разбиения
, разбиения  и выбранных точек
и выбранных точек  интегральную сумму
интегральную сумму  , где
, где  обозначает объем области
обозначает объем области  такое число, что
такое число, что 
 . Тогда мы говорим, что
. Тогда мы говорим, что  интегрируема на
интегрируема на  есть интеграл
есть интеграл 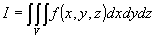 .
.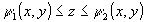 ,
, 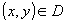 .
.  - квадрируемая область на плоскости,
- квадрируемая область на плоскости,  - непрерывные. Тогда
- непрерывные. Тогда 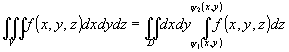
 , где
, где  - непрерывные функции, то
- непрерывные функции, то 
 устанавливает взаимно однозначное соответствие между областями
устанавливает взаимно однозначное соответствие между областями  и
и 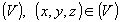 , причем функции
, причем функции  - непрерывно дифференцируемые и
- непрерывно дифференцируемые и  ни в одной точке
ни в одной точке  . Пусть
. Пусть 



