Решение. Параметрические уравнения этой линии: x=2t+1, y=t+2, z=3t-1, (0≤t≤1)Уравнение прямой АВ:
Параметрические уравнения этой линии: x=2t+1, y=t+2, z=3t-1, (0≤t≤1). Следовательно
Возможен другой способ: если принять за параметр какую-либо из координат, скажем, у, то параметрические уравнения прямой примут вид: x=2y-3, y=y, z=3y-7,
и, следовательно,
17 Формула Грина
18 Условия независимости криволинейного интеграла от пути интегрирования Как мы видели, вычисление криволинейного интеграла
непосредственно зависит от самой линии L, отсюда и величина его зависит от вида кривой. Поставим задачу: выяснить условия, при которых бы криволинейный интеграл не зависел от пути интегрирования, а только от его начальной и конечной точек. Так, с точки зрения механики независимость линейного интеграла от линии интегрирования будет обозначать, что величина работы в силовом поле
не зависит от формы пути, а только от его начальной и конечной точек. Лемма. Для того, чтобы криволинейный интеграл
в некоторой области D плоскости хоу не зависел от пути интегрирования, необходимо и достаточно, чтобы интеграл по любому замкнутому контуру, лежащему в этой области, был равен нулю.
|
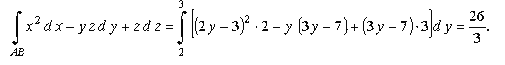
с непрерывными частными производными первого порядка 
. Тогда справедлива формула Грина
где символ 
указывает, что кривая (контур) C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки. Если 
, то формула Грина принимает вид
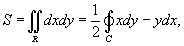где S − это площадь области R, ограниченной контуром C. Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля. Пусть векторное поле описывается функцией
Ротором или вихрем векторного поля 
называется вектор, обозначаемый 
или 
и равный
Формула Грина в векторной форме записывается в виде
Заметим, что формула Грина вытекает из "теоремы Стокса" при переходе от трехмерного случая к случаю двух координат.
, где кривая C − окружность радиуса R.
Решение.
Запишем компоненты векторного поля:
С помощью формулы Грина
преобразуем криволинейный интеграл в двойной:
Переходя к полярным координатам, находим искомый интеграл:
