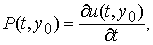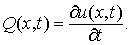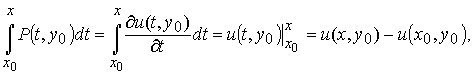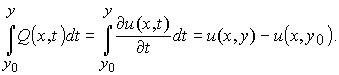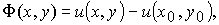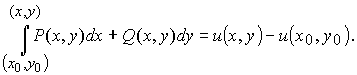Доказательство. · Необходимость.Пусть Pdx + Qdy = du(x, y)
· Необходимость. Пусть Pdx + Qdy = du (x, y). Тогда справедливо соответствие
Продифференцируем каждое из этих равенств:
По свойству смешанных производных правые части последних соотношений равны и, в силу их непрерывности (по условию теоремы), в любой точке области D выполняется равенство
Необходимость доказана. · Достаточность. Пусть в области D выполняется тождественное равенство
Но тогда по теореме 1 линейный интеграл (15) не зависит от пути интегрирования. Установим правило нахождения первообразной функции u (х, у) по её полному дифференциалу, тем самым доказав её существование. Выберем в области D какую-то фиксированную точку А (х 0, у 0) и переменную точку М (х, у). Линейный интеграл (15) будет функцией верхнего предела
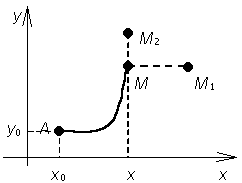
§ Пусть точка М переместилась (см. рис. 10) в положение M 1(x +
Поскольку переменная у не получила приращения на отрезке ММ 1 (
Применим к нему теорему о среднем:
где Разделив на
или, переходя к пределу при
§ Пусть теперь точка М движется параллельно оси оу, т. е. функция Ф(х, у) получает приращение по переменной у, при этом
где М 2(х, у + Проводя рассуждения, аналогичные предыдущим, приходим к заключению, что
Сложив результаты, получаем формулу полного дифференциала некоторой функции Ф(х, у)
Интегрируя, находим одну из первообразных линейного интеграла
Сформулируем правило отыскания функции. Поскольку подынтегральное выражение - полный дифференциал некоторой функции, линейный интеграл не зависит от пути интегрирования. Выберем самый удобный путь, соединяющий точки А (х 0, у 0) и М (х, у), например, ломаную АВМ с отрезками, параллельными осям (см. рис. 11). Исследуем эти отрезки:
Переходим к вычислению интеграла
Теорема доказана. Мы получили метод отыскания функции поеё полному дифференциалу, доказав таким образом факт существования такой функции. Последнюю формулу чаще записывают в виде
Получим ещё один результат, проанализировав формулу (21), каждое слагаемое которой является определённым интегралом с переменным верхним пределом, подынтегральное выражение каждого из них зависит от переменной t. Применим к ним формулу Ньютона-Лейбница, учитывая, что подынтегральное выражение криволинейного интеграла в левой части равенства есть полный дифференциал некоторой функции, т. е.
Откуда следует, что
Тогда
Следовательно,
или
Последнее равенство является формулой Ньютона-Лейбница для криволинейного интеграла, подтверждающей вывод: интеграл от полного дифференциала не зависит от пути интегрирования, а зависит только от начальной и конечной точек интегрирования.
19 Поверхностный интеграл.
|

 и
и 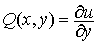 .
.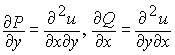 .
.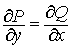 .
.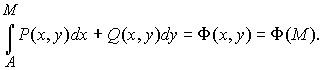
 x, y). Тогда функция Ф(х, у) получит частное приращение по переменной х
x, y). Тогда функция Ф(х, у) получит частное приращение по переменной х (20)
(20)

 .
.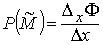
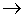 0, в силу непрерывности функции Р (х, у), имеем
0, в силу непрерывности функции Р (х, у), имеем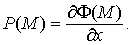
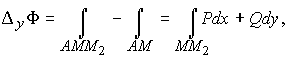
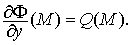




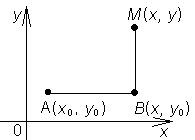
 (21)
(21) (22)
(22)