Обобщенно - однородные уравнения.
Рассмотрим уравнения вида
Уравнение (5) называется обобщенно - однородным, если существуют числа k и m такие, что
С помощью замены (при x<0 полагаем
где t - новая независимая переменная, u - новая искомая функция, уравнение (5) приводит к уравнению, не содержащему независимой переменной t и, следовательно, допускающему понижение порядка на единицу (см. п. 2). Производные при данной замене преобразуются по формулам
......................................................................
Подстановка последних равенств в (5) дает уравнение вида
которое явно не содержит независимую переменную t. Пример 4. Решить уравнение Решение. Проверим, что уравнение является однородным. С этой целью вместо переменных
Очевидно, что такое тождество выполняется лишь при условии 4k=2, т.е при k=1/2 (при этом m=2). Следовательно, данное уравнение обобщенно однородное. Применив подстановку
Последнее уравнение явно не содержит переменную t, поэтому посредством замены
Проинтегрировав последнее уравнение, находим
Далее, интегрируем уравнение
и получаем окончательно решения уравнение в виде
|
. (5)
.
)
,
.
,
.
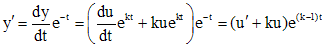
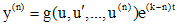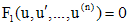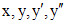подставим в выражение для функции 
соответственно 
и, если это возможно, подберем значение k таким образом, чтобы выполнялось тождество
.
, получим уравнение
.
понижаем порядок на единицу: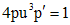
.
.
:
.
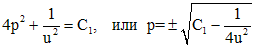