Решение. Другими словами, нам требуется найти частное решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами
Другими словами, нам требуется найти частное решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами Сначала найдем общее решение ЛНДУ, далее займемся частным решением. Мы знаем, что общее решение линейного неоднородного уравнения представляет собой сумму общего решения соответствующего однородного уравнения Найдем
Корни действительные и различные, поэтому, Переходим к
Приравнивая коэффициенты при одинаковых показателях степени x, приходим к системе линейных уравнений Это есть общее решение исходного линейного неоднородного дифференциального уравнения. Осталось найти частное решение, удовлетворяющее начальным условиям Имеем
С другой стороны Таким образом, получаем систему уравнений
34 Системы линейных дифференциальных уравнений с постоянными коэффициентами. истема дифференциальных уравнений 1-го порядка в нормальной форме записи имеет вид
Здесь u — n -мерный вектор, A — матрица n × n, элементы которой являются константами. Для нахождения решения системы (1) необходимо определить собственные числа матрицы A, т.е. корни характеристического уравнения det (A – λ E) = 0. По основной теореме алгебры это уравнение имеет ровно n корней с учётом кратности. Если все корни λ k, k = 1, n, различны между собой, то общее решение системы (1) можно представить в виде
где h k — любой собственный вектор матрицы A, соответствующий собственному числу λ k (т.е. h k — любой ненулевой вектор, являющийся решением вырожденной системы уравнений(A – λ kE) h k = 0), Ck — произвольные константы. Случай кратных корней более интересен. Если корень λ имеет кратность m, то его вклад в решение (2) зависит от ответа на вопрос: «Можно ли найти m линейно независимых собственных векторов для этого корня?», а этот ответ, в свою очередь, зависит от ответа на вопрос: «Чему равен ранг матрицы (A – λ E)?».
Возвращаемся к рассмотрению случая кратных корней. Итак, пусть собственное число λ исходной n × n -матрицы A имеет кратность m. При этом rank(A – λ E) мы знаем. Тогда число линейно независимых векторов для λ равно n – rank(A – λ E). Если m = n – rank(A – λ E), т.е. найдётся m ЛНЗ собственных векторов h 1, h 2,..., h m, то форма решения (2) не меняется: вклад собственного числа λ в решение u (t) имеет вид
Если же n – rank(A – λ E) < m, т.е. количество ЛНЗ векторов меньше, чем надо, то вклад числа λ в решение u (t) будет следующим:
Здесь степень s многочлена в скобках есть разность между кратностью корня λ и числом ЛНЗ собственных векторов для него (т.е. s = m – n + rank(A – λ E)). При этом произвольные постоянные входят в состав векторов h k (т.е. здесь требуется искать не какое-то частное решение соответствующей вырожденной системы, а общее). Нахождение векторов h k осуществляется с помощьюподстановки (4) в уравнение (1). 806. Решить систему уравнений
Характеристические числа в данном случае известны: λ1=3, λ2,3=–1. Решение. [· · ·] 811. Решить систему уравнений
Решение. [· · ·] Необходимо отметить, что в случаях, подобных вышеизложенному (т.е. когда число ЛНЗ собственных векторов меньше кратности собственного числа), имеется и другой способ нахождения решения. Этот способ основан на построении линейно независимых серий векторов (см. дайджест у Филиппова, подробности — у Понтрягина). Мне он кажется неоправданно громоздким для такой простой задачи, хотя и красивым в теоретическом плане. Однако, если в будущем предвидится необходимость в массовом решении дифференциальных систем или хочется довести своё умение решать подобные задачи до автоматизма и, заодно, свести к минимуму времязатраты (впрочем, шансов сравняться по этому показателю с Maple никаких), то понтрягинский подход можно выучить. А так, достаточно запомнить просто принцип: 1. вклад собственного числа λ в общее решение — это многочлен степени «кратность λ минус число соответствующих ЛНЗ собственных векторов», умноженный на e λ t ; 2. если подставить такое произведение в исходную систему, то можно найти коэффициенты-векторы многочлена; 3. искать коэффициенты-векторы надо в общем виде (частных решений не достаточно) и последовательно, начиная с коэффициента при старшей степени многочлена.
39 Признак Даламбера сходимости числового ряда Пусть задана бесконечная последовательность чисел
|

 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  .
. и какого-либо частного решения неоднородного уравнения
и какого-либо частного решения неоднородного уравнения 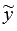 , то есть,
, то есть,  .
.
 .
.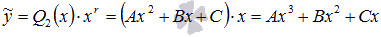 , где А, В и С – неопределенные коэффициенты. Эти коэффициенты определим из равенства
, где А, В и С – неопределенные коэффициенты. Эти коэффициенты определим из равенства  .
.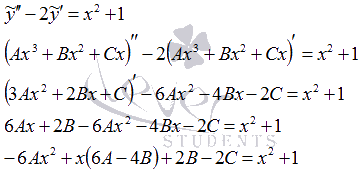
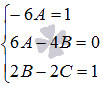 . Решая ее любым способом (при необходимости обращайтесь к статье решение систем линейных алгебраических уравнений), получаем искомые неопределенные коэффициенты
. Решая ее любым способом (при необходимости обращайтесь к статье решение систем линейных алгебраических уравнений), получаем искомые неопределенные коэффициенты  . Следовательно,
. Следовательно,  и
и 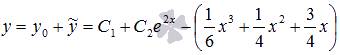 .
. , чтобы выполнялись условия
, чтобы выполнялись условия 
 . Откуда
. Откуда  . Следовательно, решением задачи Коши является функция
. Следовательно, решением задачи Коши является функция
 . Выражение
. Выражение  называется числовым рядом. При этом числа
называется числовым рядом. При этом числа  .
. -й член стремится к нулю при неограниченном возрастании
-й член стремится к нулю при неограниченном возрастании  , то ряд расходится.
, то ряд расходится. -го члена ряда к
-го члена ряда к  , т.е.
, т.е.  , то:
, то: ,
, .
.


