Остаток ряда и его оценка
Рассмотрим сходящийся числовой ряд Вычисление суммы ряда S = Определение 7. Если числовой ряд сходится, то разность Rn = S - Sn называется n -м остатком ряда. Таким образом, Rn представляет собой сходящийся числовой ряд: Rn = un+1+un+2+…. Заметим, что Абсолютная погрешность при замене суммы ряда S его частичной суммой Sn равна | Rn|=|S-Sn|. Таким образом, если требуется найти сумму ряда с точностью до E >0, то надо взять сумму такого числа n первых членов ряда, чтобы выполнялось условие | Rn|<E. Однако в общем случае находить точно Rn не удаётся. Теорема 11. (Об оценке остатка знакочередующегося числового ряда) Если знакочередующийся числовой ряд сходится по признаку Лейбница, то его n -й остаток по абсолютной величине не превосходит модуля (n +1)-го члена ряда. Доказательство. Пусть ряд u1-u2+u3-u4+…+(-1)n-1.un+… сходится по признаку Лейбница. Тогда n -й остаток ряда Rn=±(un+1-un+2+un+3-…) сам является суммой знакочередующегося числового ряда и по теореме Лейбница |Rn|≤|un+1 |. Теорема доказана. Пример. Вычислить с точностью до 0,01 сумму ряда Очевидно, ряд сходится по признаку Лейбница. u1 =
46 Понятие функционального ряда. Степенной ряд. Теорема Абеля.
О: Функциональный ряд (ф.р.) представляет собой ряд Числовым функциональный ряд можно назвать в том случае, когда В области сходимости Пример: функциональный ряд Поскольку его члены являются положительными, то для выявления области сходимости применим признак Даламбера:
если Существенный частный случай ф.р. — степенный ряд. О: Степенный ряд (с.р.) есть ф.р., который имеет следующий вид
(30.1)
Если
(30.2)
Для определения области сходимости с.р., представим доказательство теоремы Абеля. Т. (Абеля): В случае, когда степенной ряд (30.2) сходится при Предположим, что ряд Учитывая то, что функция, обладающая пределом, является ограниченной, можно обозначить
Представим ряд (30.2) в следующем виде
Для ряда, составленного из абсолютных величин его членов
(30.3)
запишем Далее предположим, что при
при нем ряд (30.2) сходится. Однако в соответствии с представленным ранее доказательством ряд (30.2) предполагает сходимость в т.
48 Применение рядов к интегрированию функций.
|

 (23)
(23) обычно технически очень сложно. Поэтому в качестве S берут S ≈ Sn. Точность этого равенства возрастает с увеличением n.
обычно технически очень сложно. Поэтому в качестве S берут S ≈ Sn. Точность этого равенства возрастает с увеличением n. Rn=
Rn= 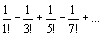
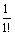 =1; u2 =
=1; u2 = 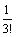 ≈
≈  ≈0,008<0,01. Поэтому S ≈1-0,166≈0,84.
≈0,008<0,01. Поэтому S ≈1-0,166≈0,84.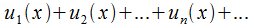 , его члены — это функции от
, его члены — это функции от 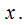
 является фиксированным. Область сходимости ф.р. есть множество
является фиксированным. Область сходимости ф.р. есть множество  значений
значений  , для которых он сходится.
, для которых он сходится.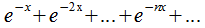 . Определить область сходимости.
. Определить область сходимости.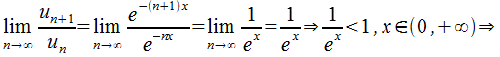
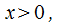 то ряд сходится.
то ряд сходится.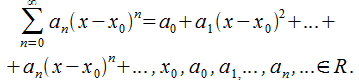
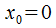 , то ряд по степеням
, то ряд по степеням 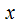 можно записать так:
можно записать так: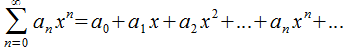
 можно заключить, что он абсолютно сходится
можно заключить, что он абсолютно сходится 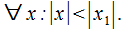 При расходимости ряда (30.2) в т.
При расходимости ряда (30.2) в т.  он расходится
он расходится  .
.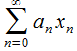 сходится, соответственно
сходится, соответственно 

 .
.
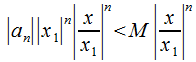 , при этом геометрическая прогрессия
, при этом геометрическая прогрессия 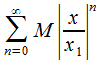 сходится при
сходится при 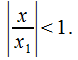 Получается, что, если
Получается, что, если  в соответствии с первым признаком сравнения ряд (30.3) сходится, то по признаку абсолютной сходимости ряд (30.2) сходится абсолютно.
в соответствии с первым признаком сравнения ряд (30.3) сходится, то по признаку абсолютной сходимости ряд (30.2) сходится абсолютно.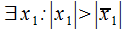 ,
,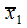 . Данное противоречие доказывает теорему.
. Данное противоречие доказывает теорему.


