Решение. Преобразуем исходный ряд:Преобразуем исходный ряд: 42 Ряд Дирихле Ряды Дирихле. Рядами Дирихле называются функциональные ряды вида S (1/ anx), где числа an неограниченно возрастают; примером ряда Дирихле может служить дзета-функция Римана
Ряды Дирихле часто используются в теории чисел.
44 Знакопеременные ряды. Достаточный признак сходимости. Определение 5. Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами. Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными рядами, так как они получаются умножением знакоположительных рядов на – 1. Изучение знакопеременных рядов начнём с частного случая – знакочередующихся рядов. Определение 6. Числовой ряд вида u1-u2+u3-u4+…+ +(- 1 )n- 1. un+ …, где un – модуль члена ряда, называется знакочередующимся числовым рядом. Теорема 9. (Признак Лейбница ) Если для знакочередующегося числового ряда Выполняются два условия: Члены ряда убывают по модулю u1 > u2 >…> un >…, то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда. Доказательство. Рассмотрим частичную сумму чётного числа членов ряда S2n = (u1-u2)+(u3-u4)+…+(u2n-1-u2n). По условию u1 > u2 >…> u2n-1 > u2n, то есть все разности в скобках положительны, следовательно, S2n возрастает с возрастанием n и S2n >0 при любом n. С другой стороны S2n = u1-[(u2-u3)+(u4-u5)+…+(u2n-2-u2n-1)+u2n]. Выражение в квадратных скобках положительно и S2n >0, поэтому S2n < u1 для любого n. Таким образом, последовательность частичных сумм S2n возрастает и ограничена, следовательно, существует конечный Рассмотрим теперь частичную сумму нечётного числа членов ряда S2n+1 = S2n + u2n+1. Перейдём в последнем равенстве к пределу при n→∞: Пример. Исследовать на сходимость ряд Применим признак Лейбница. un = Оба условия признака Лейбница выполняются, следовательно, ряд сходится. Замечания. 1. Теорема Лейбница справедлива и если условие un>un+ 1 выполняется, начиная с некоторого номера N. 2. Условие un>un+1 не является необходимым. Ряд может сходиться, если оно не выполняется. Например, ряд Определение 8. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин членов этого ряда, расходится, то говорят, что знакопеременный ряд сходится условно. Определение 9. Если сходится и сам знакопеременный ряд и ряд, составленный из абсолютных величин его членов, то говорят, что знакопеременный ряд сходится абсолютно. Пример. Установить характер сходимости ряда Очевидно, что данный ряд сходится по признаку Лейбница. Действительно: Ряд, составленный из абсолютных величин членов данного ряда Теорема 10. (Достаточный признак сходимости знакопеременного ряда или признак абсолютной сходимости) Пусть u1+u2+…+un +…= знакопеременный ряд и пусть сходится ряд, составленный из абсолютных величин его членов │ u1 │+│ u2 │+…+│ un │+…= Тогда ряд (20) тоже сходится. Доказательство. Рассмотрим вспомогательный ряд (u1 +│ u1 │)+(u2 +│ u2 │)+…+(un +│ un │)+…= Очевидно, 0≤ un +│ un │≤2│ u n│ при всех n =1, 2, …. Ряд (21) сходится по условию, поэтому сходится ряд Замечание. Обратное утверждение неверно. Если данный ряд сходится, то ряд, составленный из абсолютных величин его членов, может и расходиться. Например, ряд
|
. Таким образом, мы получили сумму двух числовых рядов 
и 
, причем каждый из них сходится (смотрите предыдущий пример). Следовательно, в силу третьего свойства сходящихся числовых рядов, сходится и исходный ряд.
(19)
S2n = S. При этом 0< S ≤ u1.
> un+1 =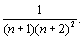 
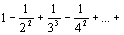
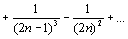сходится, как разность двух сходящихся рядов 
хотя условие un>un+1 не выполняется.
и un = 
является расходящимся гармоническим рядом. Поэтому данный ряд сходится условно.
(20)
│ un │. (21)
(un +│ un │). (22)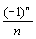
сходится по признаку Лейбница, а ряд 
расходится (это гармонический ряд).
