Рассмотрим двустороннюю поверхность  , гладкую или кусочно-гладкую, и фиксируем какую-либо из двух ее сторон, что равносильно выбору на поверхности определенной ориентации.
, гладкую или кусочно-гладкую, и фиксируем какую-либо из двух ее сторон, что равносильно выбору на поверхности определенной ориентации.
Для определенности предположим сначала, что поверхность задана явным уравнением  причем точка
причем точка  изменяется в области
изменяется в области  на плоскости
на плоскости  , ограниченный кусочно-гладким контуром.
, ограниченный кусочно-гладким контуром.
Пусть теперь в точках данной поверхности  определена некоторая функция
определена некоторая функция  . Разбив поверхность сетью кусочно-гладких кривых на части
. Разбив поверхность сетью кусочно-гладких кривых на части  и выбрав на каждой такой части точку
и выбрав на каждой такой части точку  вычисляем значение функции
вычисляем значение функции  в данной точке и умножим его на площадь
в данной точке и умножим его на площадь  проекции на плоскость
проекции на плоскость  элемента
элемента  , снабженную определенным знаком. Составим интегральную сумму:
, снабженную определенным знаком. Составим интегральную сумму:
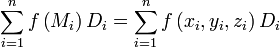 .
.
Конечный предел этой интегральной суммы при стремлении диаметров всех частей к нулю называют поверхностным интегралом второго рода от
 ,
,
распространенным на выбранную сторону поверхности  , и обозначают символом
, и обозначают символом
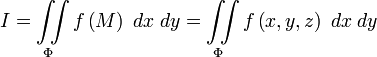
(здесь 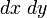 ) напоминает о площади проекции элемента поверхности на плоскость
) напоминает о площади проекции элемента поверхности на плоскость 
Если вместо плоскости  спроектировать элементы поверхности на плоскость
спроектировать элементы поверхности на плоскость  или
или  , то получим два других поверхностных интеграла второго типа:
, то получим два других поверхностных интеграла второго типа:
 или
или  .
.
В приложениях чаще всего встречаются соединения интегралов всех этих видов:
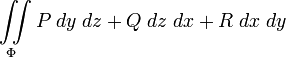
где  суть функции от
суть функции от  , определенные в точках поверхности
, определенные в точках поверхности  .
.

 , гладкую или кусочно-гладкую, и фиксируем какую-либо из двух ее сторон, что равносильно выбору на поверхности определенной ориентации.
, гладкую или кусочно-гладкую, и фиксируем какую-либо из двух ее сторон, что равносильно выбору на поверхности определенной ориентации. причем точка
причем точка  изменяется в области
изменяется в области  на плоскости
на плоскости  , ограниченный кусочно-гладким контуром.
, ограниченный кусочно-гладким контуром. . Разбив поверхность сетью кусочно-гладких кривых на части
. Разбив поверхность сетью кусочно-гладких кривых на части  и выбрав на каждой такой части точку
и выбрав на каждой такой части точку  вычисляем значение функции
вычисляем значение функции  в данной точке и умножим его на площадь
в данной точке и умножим его на площадь  проекции на плоскость
проекции на плоскость  , снабженную определенным знаком. Составим интегральную сумму:
, снабженную определенным знаком. Составим интегральную сумму: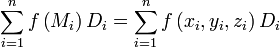 .
. ,
,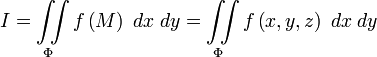
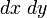 ) напоминает о площади проекции элемента поверхности на плоскость
) напоминает о площади проекции элемента поверхности на плоскость 
 или
или  , то получим два других поверхностных интеграла второго типа:
, то получим два других поверхностных интеграла второго типа: или
или  .
.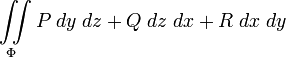
 суть функции от
суть функции от  , определенные в точках поверхности
, определенные в точках поверхности 


