Доказательство. · Достаточность. Пусть интеграл
· Достаточность. Пусть интеграл
где L - любой замкнутый контур, принадлежащий области D. Покажем, что этот интеграл не зависит от пути интегрирования. Действительно, пусть А и В - две точки области D. Соединим их двумя различными, произвольно выбранными кривыми АтВ и АпВ, лежащими в области D (рис. 8). Покажем, что
Дуги АтВ и АпВ образуют замкнутый контур АтВnA. По свойствам (3 и 1) криволинейных интегралов
Следовательно,
т. е. криволинейный интеграл не зависит о пути интегрирования. · Необходимость. Пусть в области D криволинейный интеграл
не зависит от пути интегрирования. Покажем, что интеграл по любому замкнутому контуру, лежащему в этой области, равен нулю. Действительно, рассмотрим произвольный замкнутый контур, лежащий в области D, и возьмём на нём две произвольные точки А и В (рис. 7.). Тогда
т.к. по условию
Итак, интеграл по любому замкнутому контуру L, лежащему в области D, равен нулю. Лемма доказана. Докажем теперь основную теорему. Теорема 3. Пусть функции Р (х, у) и Q (x, y) непрерывны вместе со своими частными производными первого порядка в области D, ограниченной одним замкнутым контуром. Тогда для того, чтобы криволинейный интеграл
не зависел от линии интегрирования, необходимо и достаточно, чтобы во всех точках области D выполнялось равенство
|

 ,
, .
.
 .
.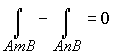 , или
, или 
 ,
, (15)
(15)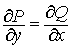 (16)
(16)


