Доказательство
· Достаточность. Пусть равенство (16) выполняется в области D. Докажем, что криволинейный интеграл (15) по любому замкнутому контуру L, лежащему в области D, равен нулю. Возьмём произвольный замкнутый контур L*, ограничивающий область D*, целиком лежащей внутри области D, и применим к нему формулу Грина
Так как по условию · Необходимость. Пусть интеграл
не зависит от пути интегрирования. Надо доказать, что выполняется равенство (16), что, в свою очередь, вызывает равенство нулю двойного интеграла (по теореме Грина)
Воспользуемся методом доказательства “от противного”. Предположим, что равенства (16) и (17) не выполняются, т.е. в области D, ограниченной контуром L, нашлась какая-то точка М, в которой
Пусть для определённости эта разность положительна. Тогда, в силу непрерывности частных производных, эта разность знакопостоянна в некоторой окрестности точки М и сохраняет тот же знак, что и в самой точке. Обозначим эту окрестность D*, а ограничивающий её контур есть L* (см рис. 9). Составим двойной интеграл по области D* от разности (18). По свойству (cм. гл. 12) интеграл сохранит знак подынтегральной функции
По формуле Грина тогда и линейный интеграл (15) будет иметь этот же знак:
Но это обозначает, что криволинейный интеграл по замкнутому контуру отличен от нуля, т.е. зависит от пути интегрирования, что противоречит исходному условию. Отсюда следует, что наше предположение неверно. Теорема доказана. Заметим, что дифференциальное выражение P (x, y) dx + Q (x, y) dy (19) напоминает форму полного дифференциала первого порядка функции двух переменных u (x, y)
Выясним условия, при которых возможно совпадение этих формул, т.е. выполнение равенства
Теорема 4 (о нахождении функции по полному дифференциалу). Если функции P (x, y), Q (x, y) определены и непрерывны в области D плоскости хоу и имеют в ней непрерывные частные производные дифференциалом некоторой функции u (х, у) тогда и только тогда, когда выполняется условие
|


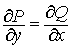 , то двойной интеграл равен рулю. Следовательно, равен нулю и криволинейный интеграл по контуру L*, что и требовалось доказать.
, то двойной интеграл равен рулю. Следовательно, равен нулю и криволинейный интеграл по контуру L*, что и требовалось доказать.
 (17)
(17) (18)
(18)


 .
.
 , то выражение Pdx + Qdy является полным
, то выражение Pdx + Qdy является полным


